
【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)将三角板放置到如图所示位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

【答案】(1)45°;(2)∠AOM=2∠NOC,理由见解析..
【解析】
(1)由∠BON=2∠NOC,OC平分∠MOB可得∠MOC=∠BOC=3∠NOC,然后利用角的倍分关系即可求解;
(2)令∠NOC为β,∠AOM为γ,∠MOC=90°-β,根据∠AOM+∠MOC+∠BOC=180°即可得到∠AOM与∠NOC满足的数量关系.
解:(1)∵∠BON=2∠NOC,OC平分∠MOB,
∴∠MOC=∠BOC=3∠NOC,
∵∠MOC+∠NOC=∠MON=90°,
∴3∠NOC+∠NOC=90°,
∴4∠NOC=90°,
∴∠BON=2∠NOC=45°,
∴∠AOM=180°﹣∠MON﹣∠BON=180°﹣90°﹣45°=45°;
(2)∠AOM=2∠NOC.
令∠NOC为β,∠AOM为γ,∠MOC=90°﹣β,
∵∠AOM+∠MOC+∠BOC=180°,
∴γ+90°﹣β+90°﹣β=180°,
∴γ﹣2β=0,即γ=2β,
∴∠AOM=2∠NOC.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.
(1)点C的坐标为 (用字母n表示)
(2)如果△ABC的面积为5.5,求n的值;
(3)在(2)的条件下,坐标平面内是否存在一点M,使以点M、A、B为顶点组成的三角形与△ABC全等?如果存在画出符合要求的图形,求出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
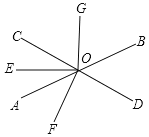
【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:

(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1 100 | 1 400 |
销售价格(元) | 今年的销售价格 | 2 000 |
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
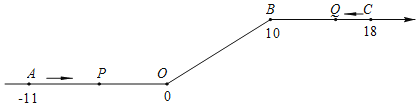
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com