Question

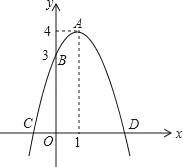
【题目】如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C、D两点.点P是x轴上的一个动点.

(1)求此抛物线的解析式；

(2)当PA+PB的值最小时，求点P的坐标.

Answer 1

【答案】(1) y=-x2+2x+3.(2)( ,0)

【解析】试题分析：

（1）由题意可设抛物线解析式为“顶点式”，再代入点B的坐标可求得解析式；

（2）由题意作出点B关于轴的对称轴点E，连接AE交轴于点P，P为所求的点，由A、E的坐标可求得直线AE的解析式，再由AE的解析式就可求得点P的坐标.

试题解析：

(1)∵抛物线的顶点A的坐标为（1，4），

∴设抛物线的表达式为y＝a(x－1)2＋4.

∵抛物线过点B(0，3)，

∴3＝a(0－1)2＋4.

解得a＝－1.

∴二次函数的表达式为y＝－(x－1)2＋4，即y＝－x2＋2x＋3.

(2)作点B关于x轴的对称点E(0，－3)，

连接AE交x轴于点P，点P即为所求点．

设AE所在直线的表达式为y＝kx＋b，

分别代入A，E坐标，得，解得，

∴y＝7x－3.

当y＝0时，x＝.

∴点P的坐标为(，0)．