
【题目】某海船以![]() 海里/小时的速度向北偏东70°方向行驶,在A处看见灯塔B在海船的北偏东40°方向,5小时后船行驶到C处,发现此时灯塔B在海船的北偏西65°方向,求此时灯塔B到C处的距离。
海里/小时的速度向北偏东70°方向行驶,在A处看见灯塔B在海船的北偏东40°方向,5小时后船行驶到C处,发现此时灯塔B在海船的北偏西65°方向,求此时灯塔B到C处的距离。

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
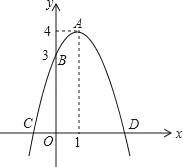
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PA切⊙O于点A,过点P的任一直线交⊙O于B、C,连结AB、AC,连PO交⊙O于D、E.
(1)求证:∠PAB=∠C.
(2)如果PA2=PD·PE,那么当PA=2,PD=1时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△A'B'C',∠A=∠A',∠B=∠B',∠C=50°,AB=18cm,则∠C'=___________,A'B'=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com