Question

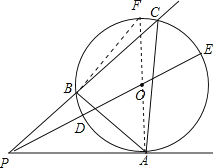
【题目】如图，P为⊙O外一点，PA切⊙O于点A，过点P的任一直线交⊙O于B、C，连结AB、AC，连PO交⊙O于D、E．

（1）求证：∠PAB=∠C．

（2）如果PA2=PD·PE，那么当PA=2，PD=1时，求⊙O的半径．

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）过A点作直径AF，连接BF，求得∠ABF＝90°，即∠F＋∠BAF＝90°，PA切⊙O于点A．得出∠PAF＝90°，即∠PAB＋∠BAF＝90°，从而求得∠PAB＝∠F，根据同弧所对的圆周角相等得出∠F＝∠C，进而求得∠PAB＝∠C；

（2）由PA2＝PDPE求得PE＝4，因为DE＝PE－PD，即可求得圆的直径，从而求得圆的半径．

试题解析：

（1）证明：过A点作直径AF，连接BF，

∴∠ABF＝90°，

∴∠F＋∠BAF＝90°，

∵PA切⊙O于点A．

∴∠PAF＝90°，

∴∠PAB＋∠BAF＝90°

∴∠PAB＝∠F，

∵∠F＝∠C，

∴∠PAB＝∠C；

（2）解：∴PA2＝PDPE，

∵PA＝2，PD＝1，

∴PE＝4，

∴DE＝PE－PD＝4－1＝3，

∴OD＝OE＝，

∴⊙O的半径为；