
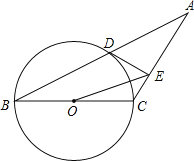
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=8,求△OEC的面积.
【答案】(1)证明见解析;(2)S△OEC=2![]() .
.
【解析】试题(1)由△ABC 是等腰三角形,可得CA=CB,则∠A = ∠B,又由OD=OB,可得∠ODB = ∠B,所以∠A = ∠ODB,即OD ∥AC,又OD⊥DE, AC⊥DE,所以DE是⊙O的切线继而可证得结论;(2)连接DC.首先证△ODC为等边三角形,再根据三角函数的性质,求得AD、CD、ED、AE、EC的长,然后求得S△OEC =![]() OCEF.
OCEF.
∵OB=OD,
∴∠OBD=∠ODB.
又∵∠A=∠B=30°
∴∠A=∠ODB,
∴DO∥AC
∵DE⊥AC
∴OD⊥DE.
∴DE为⊙O的切线.
(2)连接DC.
∵∠OBD=∠ODB=30°,
∴∠DOC=60°.
∴△ODC为等边三角形.
∴∠ODC=60°,
∴∠CDE=30°
又∵BC=8,
∴DC=4,
∴CE=2.
过点E作EF⊥BC,交BC的延长线于点F.
∵∠ECF=∠A+∠B=60°,
∴EF=CE·sin60°=2×![]() =
=![]()
∴S△OEC =![]() OCEF=
OCEF=![]() ×4×
×4×![]() =2
=2![]() .
.
故答案为:


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
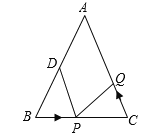
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
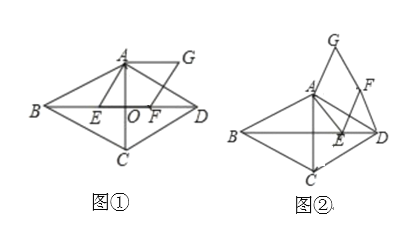
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正整数a,我们规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=![]() .例如f(15)=3×15+1=46,f(8)=
.例如f(15)=3×15+1=46,f(8)=![]() =4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
=4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司员工住在![]() 三个住宅区,已知
三个住宅区,已知![]() 区有2人,
区有2人,![]() 区有7人,
区有7人,![]() 区有12人,三个住宅区在同一条直线上,且
区有12人,三个住宅区在同一条直线上,且![]() ,
,![]() 是
是![]() 的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在
的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在![]() 四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
![]()
A.![]() 处B.
处B.![]() 处C.
处C.![]() 处D.
处D.![]() 处
处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 阅读理解
问题1:已知a、b、c、d为正数,![]() ,ac=bd,试说明a=d,b=c.
,ac=bd,试说明a=d,b=c.
我们通过构造几何模型解决代数问题. 注意到条件![]() ,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
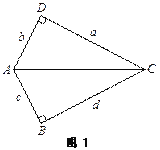
∵ac=bd,
∴AB·CD=BC·AD
∴![]()
请你按照以上思路继续完成说明.
⑵ 深入探究
问题2:若a>0,b>0,试比较![]() 和
和![]() 的大小.
的大小.
为此我们构造图2所示的几何模型,其中AB为直径, O为圆心,点C在半圆上,CD⊥AB 于D,AD=a,BD=b.
请你利用图2所示的几何模型解决提出的问题2.
⑶ 拓展运用
对于函数y=x+![]() ,求当x>0时,求y的取值范围.
,求当x>0时,求y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com