
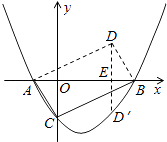
【题目】如图,抛物线y= ![]() x2﹣x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=﹣2x上.
x2﹣x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=﹣2x上.
(1)求a的值;
(2)求A,B的坐标;
(3)以AC,CB为一组邻边作ACBD,则点D关于x轴的对称点D′是否在该抛物线上?请说明理由.
【答案】
(1)
解:∵抛物线y= ![]() x2﹣x+a其顶点在直线y=﹣2x上.
x2﹣x+a其顶点在直线y=﹣2x上.
∴抛物线y= ![]() x2﹣x+a,
x2﹣x+a,
= ![]() (x2﹣2x)+a,
(x2﹣2x)+a,
= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() +a,
+a,
∴顶点坐标为:(1,﹣ ![]() +a),
+a),
∴y=﹣2x,﹣ ![]() +a=﹣2×1,
+a=﹣2×1,
∴a=﹣ ![]()
(2)
解:二次函数解析式为:y= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
∵抛物线y= ![]() x2﹣x﹣
x2﹣x﹣ ![]() 与x轴交于点A,B,
与x轴交于点A,B,
∴0= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
整理得:x2﹣2x﹣3=0,
解得:x=﹣1或3,
A(﹣1,0),B(3,0)
(3)
解:作出平行四边形ACBD,作DE⊥AB,
在△AOC和△BDE中
∵ 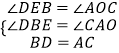
∴△AOC≌△BED(AAS),
∵AO=1,
∴BE=1,
∵二次函数解析式为:y= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
∴图象与y轴交点坐标为:(0,﹣ ![]() ),
),
∴CO= ![]() ,∴DE=
,∴DE= ![]() ,
,
D点的坐标为:(2, ![]() ),
),
∴点D关于x轴的对称点D′坐标为:(2,﹣ ![]() ),
),
代入解析式y= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
∵左边=﹣ ![]() ,右边=
,右边= ![]() ×4﹣2﹣
×4﹣2﹣ ![]() =﹣
=﹣ ![]() ,
,
∴D′点在函数图象上.
【解析】(1)根据二次函数的顶点坐标的求法得出顶点坐标,再代入一次函数即可求出a的值;(2)根据二次函数解析式求出与x轴的交点坐标即是A,B两点的坐标;(3)根据平行四边形的性质得出D点的坐标,即可得出D′点的坐标,即可得出答案.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. 
(1)现随机转动转盘一次,停止后,指针指向1的概率为;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1, ![]()
C.1,1, ![]()
D.1,2, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() x+b和y=x的图象于点C、D.
x+b和y=x的图象于点C、D. 
(1)求点A的坐标;
(2)若OB=CD,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正五边形ABCDE中,对角线AD,AC与EB分别相交于点M,N.下列结论错误的是( ) 
A.四边形EDCN是菱形
B.四边形MNCD是等腰梯形
C.△AEM与△CBN相似
D.△AEN与△EDM全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,正面分别写着1,2,3,4,5,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC. 
(1)求证:BC平分∠ABP;
(2)求证:PC2=PBPE;
(3)若BE﹣BP=PC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, ![]() =
= ![]()

(1)求证:OA=OB;
(2)已知AB=4 ![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com