
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣
x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣ ![]() ).直线y=mx+
).直线y=mx+ ![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.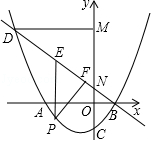
(1)求抛物线y= ![]() x2+bx+c的表达式及点D的坐标;
x2+bx+c的表达式及点D的坐标;
(2)若四边形PEMN是平行四边形?请求出点P的坐标;
(3)过点P作PF⊥BD于点F,设△PEF的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
【答案】
(1)
解:将B,C点坐标代入函数解析式,得 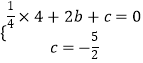 ,
,
解得 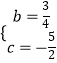 ,
,
抛物线的解析式为y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() .
.
∵直线y=mx+ ![]() 过点B(2,0),
过点B(2,0),
∴2m+ ![]() =0,
=0,
解得m=﹣ ![]() ,
,
直线的解析式为y=﹣ ![]() x+
x+ ![]() .
.
联立直线与抛物线,得 
∴ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() x+
x+ ![]() ,
,
解得x1=﹣8,x2=2(舍),
∴D(﹣8,7 ![]() )
)
(2)
解:∵DM⊥y轴,
∴M(0,7 ![]() ),N(0,
),N(0, ![]() )
)
∴MN=7 ![]() ﹣
﹣ ![]() =6.
=6.
设P的坐标为(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),E的坐标则是(x,﹣
),E的坐标则是(x,﹣ ![]() x+
x+ ![]() )
)
PE=﹣ ![]() x+
x+ ![]() ﹣(
﹣( ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() )=﹣
)=﹣ ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∵PE∥y轴,要使四边形PEMN是平行四边形,必有PE=MN,
即﹣ ![]() x2﹣
x2﹣ ![]() x+4=6,解得x1=﹣2,x2=﹣4,
x+4=6,解得x1=﹣2,x2=﹣4,
当x=﹣2时,y=﹣3,即P(﹣2,﹣3),
当x=﹣4时,y=﹣ ![]() ,即P(﹣4,﹣
,即P(﹣4,﹣ ![]() ),
),
综上所述:点P的坐标是(﹣2,﹣3)和)(﹣4,﹣ ![]() )
)
(3)
解:在Rt△DMN中,DM=8,MN=6,
由勾股定理,得
DN= ![]() =10,
=10,
∴△DMN的周长是24.
∵PE∥y轴,
∴∠PEN=∠DNM,
又∵∠PFE=∠DMN=90°,
∴△PEF∽△DMN,
∴ ![]() =
= ![]() ,
,
由(2)知PE=﹣ ![]() a2﹣
a2﹣ ![]() a+4,
a+4,
∴ ![]() =
= ![]() ,
,
∴C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
C=﹣ ![]() (a+3)2+15,
(a+3)2+15,
C与a的函数关系式为C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
当x=﹣3时,C的最大值是15
【解析】(1)根据待定系数法,可得抛物线的解析式,直线的解析式,根据解方程组,可得D点坐标;(2)根据y轴上两点间的距离是较大的纵坐标减较小的纵坐标,可得MN,PE的长,根据平行四边形的判定,可得关于x的方程,根据解方程,可得P的横坐标,根据自变量与函数值的对应关系,可得答案;(3)根据勾股定理,可得DN的长,根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,根据比例的基本性质,可得答案.
,根据比例的基本性质,可得答案.
【考点精析】掌握平行四边形的判定和相似三角形的判定与性质是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】县内某小区正在紧张建设中,现有大量的沙石需要运输,“建安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“建安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“建安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
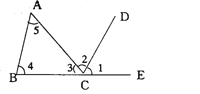
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
A,B两款手机的进货和销售价格如下表:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x﹣2经过A、C两点,且AB=2.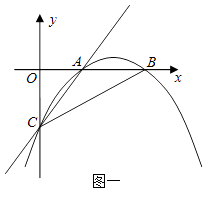
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s= ![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.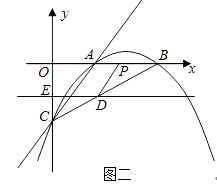
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com