
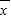 ′=
′=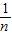 [(3x1+2)+…+(3xn+2)]=
[(3x1+2)+…+(3xn+2)]=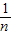 [3×(x1+x2+…+xn)+2n]=17,
[3×(x1+x2+…+xn)+2n]=17,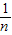 [(3x1+2-17)2+(3x2+2-17)2+…+(3xn+2-17)2]
[(3x1+2-17)2+(3x2+2-17)2+…+(3xn+2-17)2]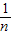 [(3x1-15)2+…+(3xn-15)2]=9×
[(3x1-15)2+…+(3xn-15)2]=9×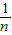 [(x1-5)2+(x2-5)2+…+(xn-5)2]=144.
[(x1-5)2+(x2-5)2+…+(xn-5)2]=144.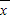 ;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.
;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数. 

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com