
【题目】如图,在平面直角坐标系中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点,以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的关系为 ;
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?请说明理由;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,求出E点所满足的函数关系式,并写出E点所经过的路径长.

【答案】(1)相等; 垂直;(2)成立,理由见解析;(3)E点坐标为(t+1,t-1),![]() ;E点所经过的路径长为
;E点所经过的路径长为![]()
【解析】
(1)连接CF,通过同角的余角相等可得∠OAD=∠CAF,由正方形性质可得AD=AF,再由已知OA=OC易证得两三角形全等,而OD=CF;由△ODA≌△CFA,所以∠FCA=∠DOA,即∠FCO=∠FCA+∠ACO=∠DOA+∠ACO,得到∠FCO=90°;
(2)按题目要求构造正方形ADEF,连接CF,利用(1)的方法证明,结论易得;
(3)分为t<1,t=1,t>1三种情况讨论.分别讨论利用全等三角形的判定和性质易得结论.根据点E的坐标可以分析出点运动的轨迹,即可求解.
(1)连接CF,如图:

∵∠OAC=90°,∠DAF=90°,
∴∠OAC=∠DAF,
∴∠OAD=∠OAC-∠CAD=∠DAF-∠CAD=∠CAF,
在△OAD和△CAF中,
 ,
,
∴△OAD≌△CAF,
∴OD=CF,∠AOD=∠ACF,
∴∠OCF=∠OCA+∠ACF=∠OCA+∠AOC,
在Rt△OAC中,
∵∠OCA+∠AOC=90°,
∴∠OCF=90°,
∴OD⊥CF,
故答案:相等; 垂直;
(2)结论依然成立,即OD=CF,OD⊥CF,理由如下: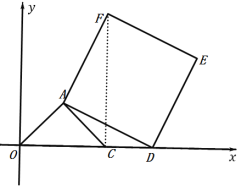
如图,连接CF.
∵∠OAC=90°,∠DAF=90°,
∴∠OAC=∠DAF,
∴∠OAD=∠OAC+∠CAD=∠DAF+∠CAD=∠CAF,
在△OAD和△CAF中,
 ,
,
∴△OAD≌△CAF,
∴OD=CF,∠AOD=∠ACF,
∴∠OCF=∠OCA+∠ACF=∠OCA+∠AOC,
在Rt△OAC中,
∵∠OCA+∠AOC=90°,
∴∠OCF=90°,
∴OD⊥CF;
(3)过点A作AG⊥x轴于G,过点E作EH⊥x轴于H,
∵OA=CA,且∠OAC=90°,
∴OG=CG=AG,
∵A的坐标为(1,1),
∴OG=AG=1,OC=2,
当D在线段OG上,如图,此时t<1,则DG=1-t,

∵∠DAG+∠ADG=90°,∠ADG+∠HDE=90°,
∴∠DAG=∠HDE,
在△ADG和△DEH中,
 ,
,
∴△ADG≌△DEH,
∵OD= t,
∴HE=DG=1-t,DH=AG=1,
∴OH=OD+DH=t+1,
∴E点坐标为(t+1,-(1-t)),即(t+1,t-1);
当D与G点重合,E点与C点重合,即E点坐标为(2,0),
此时t=1,所以E点坐标也为(t+1,t-1);
当D在线段GC上,如图,此时t>1,则DG=t-1,

∵∠ADE=90°,
∴∠ADG+∠EDH=90°,
∵∠DAG+∠ADG=90°,
∴∠DAG=∠EDH,
在△ADG和△DEH中,
 ,
,
∴△ADG≌△DEH,
∵OD= t,
∴HE=DG=t-1,DH=AG=1,
∴OH=OD+DH=t+1,
∴E点坐标为(t+1,t-1),
综上所述,E点坐标为(t+1,t-1),![]() ;
;
当t=0时,点E的坐标为![]() (1,-1),
(1,-1),
当t=2时,点E的坐标为![]() (3,1),
(3,1),
猜想点E在线段![]() 上运动,
上运动,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() (1,-1),
(1,-1),![]() (3,1)代入得:
(3,1)代入得:![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∵点E(t+1,t-1)在![]() 上,且
上,且![]() ,
,
∴点E在线段![]() 上运动,猜想正确,
上运动,猜想正确,
∴E点由![]() (1,-1)直线运动到
(1,-1)直线运动到![]() (3,1),
(3,1),
∴线段![]() ,
,
∴E点所经过的路径长为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
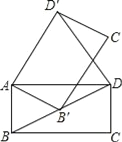
【题目】如图,在矩形ABCD中,AB=1,BC=![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() +1 D. 2
+1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() 若一元二次方程
若一元二次方程![]() 有一个根是
有一个根是![]() ,则代数式
,则代数式![]() 的值是
的值是![]()
![]() 若
若![]() ,则
,则![]() 是一元二次方程
是一元二次方程![]() 的一个根
的一个根
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有不相等的两个实数根
有不相等的两个实数根
![]() 当m取整数
当m取整数![]() 或1时,关于x的一元二次方程
或1时,关于x的一元二次方程![]() 与
与![]() 的解都是整数.
的解都是整数.
其中正确的有![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=
(k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=![]() ,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
(1)求该反比例函数和一次函数的解析式;
(2)连接ED,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校对本校的八年级学生对待学习的态度进行了一次抽样调查,结果分成“非常感兴趣”、“比较感兴趣”、“一般般”、“不感兴趣”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.


根据所给数据,解答下列问题:
(1)本次问卷共随机调查了_________名学生,扇形统计图中![]() _________,扇形
_________,扇形![]() 所对应的圆心角为_________°;
所对应的圆心角为_________°;
(2)请根据数据信息补全条形统计图;
(3)若该校有2000名学生,估计选择“非常感兴趣”、“比较感兴趣”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把符号“![]() ”读作“
”读作“![]() 的阶乘”,规定“其中
的阶乘”,规定“其中![]() 为自然数,当
为自然数,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ”.例如:
”.例如:![]() .又规定“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加碱,有括号就先算括号里面的”.按照以上的定义和运算顺序,计算:
.又规定“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加碱,有括号就先算括号里面的”.按照以上的定义和运算顺序,计算:
(1)![]() _______;
_______;
(2)![]() _______;
_______;
(3)![]() ______;
______;
(4)用具体数试验一下,看看等式![]() 是否成立?
是否成立?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com