
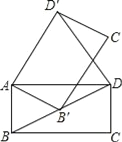
【题目】如图,在矩形ABCD中,AB=1,BC=![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() +1 D. 2
+1 D. 2
科目:初中数学 来源: 题型:
【题目】2019年国庆档上映了多部优质国产影片,其中《我和我的祖国》、《中国机长》这两部影片不管是剧情还是制作,都非常值得一看.《中国机长》是根据真实故事改编的,影片中全组机组人员以自己的实际行动捍卫安全、呵护生命,堪称是“新时代的英雄”、“民航奇迹的创造者”,据统计,某地10月1日该影片的票房约为1亿,10月3日的票房约为1.96亿.
(1)求该地这两天《中国机长》票房的平均增长率;
(2)电影《我和我的祖国》、《中国机长》的票价分别为40元、45元,10月份,某企业准备购买200张不同时段的两种电影票,预计总花费不超过8350元,其中《我和我的祖国》的票数不多于《中国机长》票数的2倍,请求出该企业最省钱的方案及所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]() ,
,
第2个等式:a2=![]() ,
,
第3个等式:a3=![]() ,
,
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+…+a2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
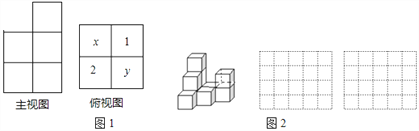
【题目】.(1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图![]() 所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则
所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则![]() ______
______
(2)如图(2),是由若干个完全相同的小正方体组成的一个几何体
①请画出这个几何体的左视图和俯视图; ![]() 用阴影表示
用阴影表示![]()
②如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加______个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方法回顾)
(1)如图1,过正方形ABCD的顶点A作一条直l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .

(问题解决)
(2)如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.
(思维拓展)
(3)如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 .(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b满足![]() .请回管问题:
.请回管问题:
(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,![]() 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.
(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)点D在线段BC上何处时,四边形CDEF是平行四边形且![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点,以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的关系为 ;
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?请说明理由;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,求出E点所满足的函数关系式,并写出E点所经过的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com