
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)点D在线段BC上何处时,四边形CDEF是平行四边形且![]() .
.

【答案】见解析
【解析】
(1)在△ACD和△CBF中,根据已知条件有两边和一夹角对应相等,可根据边角边来证明全等.
(2)当∠DEF=30°,即为∠DCF=30°,在△BCF中,∠CFB=90°,即F为AB的中点,又因为△ACD≌△CBF,所以点D为BC的中点.
证明:(1)∵△ABC为等边三角形,
∴AC=BC,∠FBC=∠DCA,
在△ACD和△CBF中,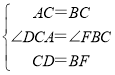 ,
,
所以△ACD≌△CBF(SAS);
(2)当D在线段BC上的中点时,四边形CDEF为平行四边形,且∠DEF=30°.
如图,连接BE,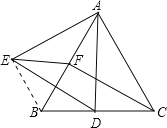
在△AEB和△ADC中,
AB=AC,∠EAB+∠BAD=∠DAC+∠BAD=60°,即∠EAB=∠DAC,AE=AD,
∴△AEB≌△ADC(SAS),
又∵△ACD≌△CBF,
∴△AEB≌△ADC≌△CFB,
∴EB=FB,∠EBA=∠ABC=60°,
∴△EFB为正三角形,
∴EF=FB=CD,∠EFB=60°,
又∵∠ABC=60°,
∴∠EFB=∠ABC=60°,
∴EF∥BC,
而CD在BC上,∴EF平行且相等于CD,
∴四边形CDEF为平行四边形,
∵D在线段BC上的中点,
∴F在线段AB上的中点,
∴∠FCD=![]() ×60°=30°
×60°=30°
则∠DEF=∠FCD=30°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x铀的一个交点在点(3,0)和(4,0)之间,则下列结论:①abc>0;②a﹣b+c>0;③b2=4a(c﹣m);④一元二次方程ax2+bx+c=m+1有两个不相等的实数根,其中正确结论的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
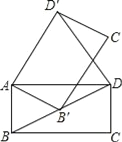
A. ![]() B.
B. ![]() C.
C. ![]() +1 D. 2
+1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x |
|
| 0 | 1 | 2 |
|
y |
| 0 | 3 | 4 | 3 |
|
那么关于它的图象,下列判断正确的是![]()
A. 开口向上 B. 与x轴的另一个交点是![]()
C. 与y轴交于负半轴 D. 在直线![]() 的左侧部分是下降的
的左侧部分是下降的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校对本校的八年级学生对待学习的态度进行了一次抽样调查,结果分成“非常感兴趣”、“比较感兴趣”、“一般般”、“不感兴趣”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.


根据所给数据,解答下列问题:
(1)本次问卷共随机调查了_________名学生,扇形统计图中![]() _________,扇形
_________,扇形![]() 所对应的圆心角为_________°;
所对应的圆心角为_________°;
(2)请根据数据信息补全条形统计图;
(3)若该校有2000名学生,估计选择“非常感兴趣”、“比较感兴趣”共约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com