
【题目】如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( ) 
A.90°
B.120°
C.135°
D.150°
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>
交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集. 
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
艾斯柯同学类比以上知识的研究方法,用函数与方程的思想对不等式的解法进行了探究,请将他下面的②③④补充完整:
①当x=0时,原不等式不成立:当x>0时,原不等式可以转化为x2+4x﹣1> ![]() ;当x<0时,原不等式可以转化为x2+4x﹣1<
;当x<0时,原不等式可以转化为x2+4x﹣1< ![]() .
.
②构造函数,画出图象
设y3=x2+4x﹣1,y4= ![]() 在同一坐标系中分别画出这两个函数的图象.
在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);
如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);
③利用图象,确定交点横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ![]()
④借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上,Rt△ABC与直径为CE的半圆O,如图1摆放,∠B=90°,BC=m,AC=2CE=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转,且∠ECD=∠ACB,旋转角记为α(0°≤α≤180°). 
(1)①当α=0°时,连接DE,则∠CDE=°,CD=;②当α=180°时, ![]() = .
= .
(2)试判断:旋转过程中 ![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)若m=4,n=5,当α=∠ACB时,线段BD= .
(4)若m=4 ![]() ,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .
,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.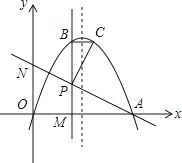
(1)a= ![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图a>1时,若AP⊥PC,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,
求证:四边形ABCD是四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为平行四边形两组对边分别相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 . 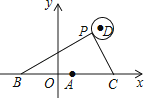
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角边长为2a的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程x2﹣6x﹣m=0有两个实数根.
(1)求m的取值范围;
(2)如果m取符合条件的最小整数,且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根,求常数n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com