
【题目】在平面上,Rt△ABC与直径为CE的半圆O,如图1摆放,∠B=90°,BC=m,AC=2CE=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转,且∠ECD=∠ACB,旋转角记为α(0°≤α≤180°). 
(1)①当α=0°时,连接DE,则∠CDE=°,CD=;②当α=180°时, ![]() = .
= .
(2)试判断:旋转过程中 ![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)若m=4,n=5,当α=∠ACB时,线段BD= .
(4)若m=4 ![]() ,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .
,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .
【答案】
(1)90;![]() m;
m;![]()
(2)如图3中,
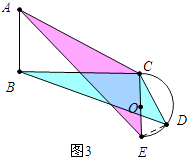
∵∠ACB=∠DCE,
∴∠ACE=∠BCD,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴△ACE∽△BCD,
∴ ![]() =
= ![]() =
= ![]() ;
;
(3)![]()
(4)2 ![]() 或
或 ![]()
【解析】(1)解:①如图1中 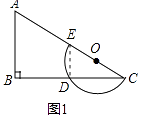
当α=0时,连接DE,则∠CDE=90°,
∵∠CDE=∠B=90°,
∴DE∥AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵BC=m,
∴CD= ![]() m,
m,
所以答案是90°, ![]() m,
m,
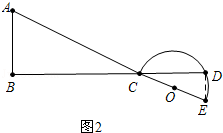
②如图2中,当α=180°时,BD=BC+CD= ![]() m,AE=AC+CE=
m,AE=AC+CE= ![]() n,
n,
∴ ![]() =
= ![]() .
.
所以答案是 ![]() ;
;
⑶如图4中,当α=∠ACB时,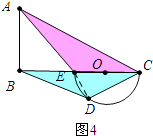
在Rt△ABC中,∵AC=5,BC=4,
∴AB= ![]() =3,
=3,
在Rt△ABE中.∵AB=3,BE=BC﹣CE=1.5,
∴AE= ![]() =
= ![]() =
= ![]() ,
,
由(2)可知△ACE∽△BCD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BD= ![]() ,
,
所以答案是 ![]() ;
;
⑷∵m=4 ![]() ,n=6,
,n=6,
∴CE=3,CD=2 ![]() ,AB=
,AB= ![]() =2,
=2,
①如图5中,当α=90°时,半圆与AC相切,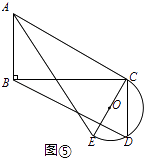
在Rt△DBC中,BD= ![]() =2
=2 ![]() .
.
②如图6中,当α=90°+∠ACB时,半圆与BC相切,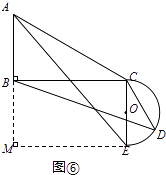
作EM⊥AB于M,
∵∠M=∠CBM=∠BCE=90°,
∴四边形BCEM是矩形,
∴BM=CE=3,ME=4 ![]() ,
,
∴AM=5,AE= ![]() =
= ![]() ,
,
由(2)可知 ![]() =
= ![]() ,
,
∴BD= ![]() .
.
所以答案是2 ![]() 或
或 ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. 
(1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; 
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在银行存入一笔零花钱.已知这种储蓄的年利率为n%,若设到期后的本息和(本金+利息)为y(元),存入的时间为x(年),那么, 
(1)下列哪个图象更能反映y与x之间的函数关系?从图中你能看出存入的本金是多少元?一年后的本息和是多少元?
(2)根据(1)的图象,求出y与x的函数关系式(不要求写出自变量x的取值范围),并求出两年后的本息和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( ) 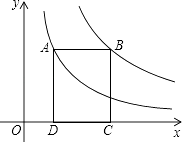
A.12
B.10
C.8
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com