
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.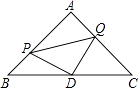
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
【答案】
(1)证明:连接AD, 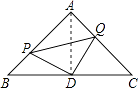
∵△ABC是等腰直角三角形,D是BC的中点
∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,
在△BPD和△AQD中,
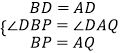 ,
,
∴△BPD≌△AQD(SAS),
∴PD=QD,∠ADQ=∠BDP,
∵∠BDP+∠ADP=90°
∴∠ADP+∠ADQ=90°,即∠PDQ=90°,
∴△PDQ为等腰直角三角形
(2)当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:
∵∠BAC=90°,AB=AC,D为BC中点,
∴AD⊥BC,AD=BD=DC,∠B=∠C=45°,
∴△ABD是等腰直角三角形,
当P为AB的中点时,DP⊥AB,即∠APD=90°,
又∵∠A=90°,∠PDQ=90°,
∴四边形APDQ为矩形,
又∵DP=AP= ![]() AB,
AB,
∴矩形APDQ为正方形(邻边相等的矩形为正方形).
【解析】(1)根据等腰三角形的性质,△ABC是等腰直角三角形,D是BC的中点,得到△BPD≌△AQD,根据全等三角形的对应边、对应角相等,得到PD=QD,∠ADQ=∠BDP,得到结论△PDQ为等腰直角三角形;(2)根据已知条件得到△ABD是等腰直角三角形,当P为AB的中点时,DP⊥AB,即∠APD=90°,又∠A=90°,∠PDQ=90°,得到四边形APDQ为矩形,由DP=AP=![]() AB,得到矩形APDQ为正方形.
AB,得到矩形APDQ为正方形.


科目:初中数学 来源: 题型:
【题目】为了进一步了解八年级500名学生的身体素质情况,体育老师对八年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示:

请结合图表完成下列问题:
(1)表中的m= , 次数在140≤x<160这组的频率为;
(2)请你把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,求八年级合格的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
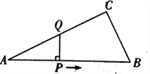
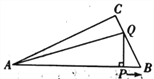
【题目】如图,△ABC中,∠ACB =90°,AB=1O, ![]() ,点P是斜边AB上一个动点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图像大致为 ( )
,点P是斜边AB上一个动点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图像大致为 ( )
A. 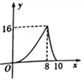 B.
B. 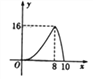 C.
C. 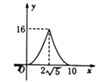 D.
D. 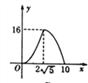
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】医学研究发现一种新病毒的直径约为0.000043毫米,则0.000043用科学记数法表示()
A. 0.43×10-4B. 43x105C. 4.3x10-4D. 4.3×10-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
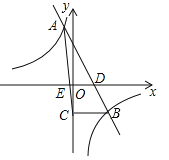
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )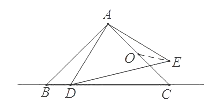
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
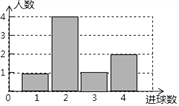
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com