
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=10,等腰直角三角形ADE绕着点A旋转,∠DAE=90°,AD=AE=6,连接BD、CD、CE,点M、P、N分别为DE、DC、BC的中点,连接MP、PN、MN,则△PMN的面积最大值为_____.

【答案】32
【解析】
由题意可证△ADB≌△EAC,可得BD=CE,∠ABD=∠ACE,由三角形中位线定理可证△MPN是等腰直角三角形,则S△PMN=![]() PN2=
PN2=![]() BD2.可得BD最大时,△PMN的面积最大,由等腰直角三角形ADE绕着点A旋转,可得D是以A为圆心,AD=6为半径的圆上一点,可求BD最大值,即可求△PMN的面积最大值.
BD2.可得BD最大时,△PMN的面积最大,由等腰直角三角形ADE绕着点A旋转,可得D是以A为圆心,AD=6为半径的圆上一点,可求BD最大值,即可求△PMN的面积最大值.
∵△ABC,△ADE是等腰直角三角形,
∴AD=AE,AB=AC,∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE且AB=AC,AD=AE,
∴△ADB≌△AEC,
∴DB=EC,∠ABD=∠ACE.
∵M,N,P分别是DE,DC,BC的中点,
∴MP∥EC,MP=![]() EC,NP=
EC,NP=![]() DB,NP∥BD,
DB,NP∥BD,
∴MP=NP,∠DPM=∠DCE,∠PNC=∠DBC.
设∠ACE=x°,∠ACD=y°,
∴∠ABD=x°,∠DBC=45°﹣x°=∠PNC,∠DCB=45°﹣y°,
∴∠DPM=x°+y°,∠DPN=∠DCB+∠PNC=∠DCB+∠DBC=45°﹣y°+45°﹣x°=90°﹣x°﹣y°,
∴∠MPN=90°且PN=PM,
∴△PMN是等腰直角三角形,∴S△PMN=![]() PN2=
PN2=![]() BD2,∴当BD最大时,△PMN的面积最大.
BD2,∴当BD最大时,△PMN的面积最大.
∵D是以A点为圆心,AD=6为半径的圆上一点,
∴A,B,D共线且D在BA的延长线时,BD最大.
此时BD=AB+AD=16,
∴△PMN的面积最大值为32.
故答案为:32.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图是一个多面体的表面展开图,每个面上都标注了字母(字母在多面体的外表面),请根据要求回答问题.

(1)如果D面在多面体的左面,那么F面在哪里?
(2)B面和哪一面是相对的面?
(3)如果C面在前面,从上面看到的是D面,那么从左面能看到哪一面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解答后面给出的问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如![]() 与
与![]() ,
,![]() +1与
+1与![]() -1.
-1.
(1)请你再写出两个含有二次根式的代数式,使它们互为有理化因式:__________________;
这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:![]() ,
,![]() .
.
(2)请仿照上面给出的方法化简:![]() ;
;
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
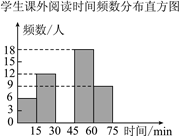
【题目】某校要了解学生每天的课外阅读时间情况,随机调查了部分学生,对学生每天的课外阅读时间x(单位:min)进行分组整理,并绘制了如图所示的不完整的统计图表,根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了________名学生;
(2)统计表中a=________,b=________;
(3)将频数分布直方图补充完整;
(4)若全校共有1200名学生,请估计阅读时间不少于45 min的有多少人.
课外阅读时间x/min | 频数/人 | 百分比 |
0≤x<15 | 6 | 10% |
15≤x<30 | 12 | 20% |
30≤x<45 | a | 25% |
45≤x<60 | 18 | b |
60≤x<75 | 9 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:
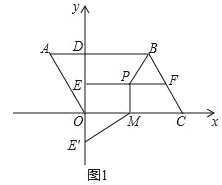
【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
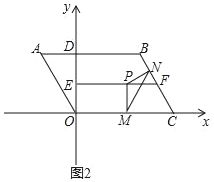
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( ) 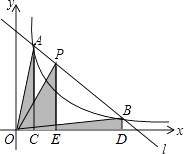
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习代数式的值时,介绍了计算程序中的框图:用“![]() ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“![]() ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“![]() ”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的
”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的![]() 为正整数).
为正整数).
例如:输入![]() ,结果依次为
,结果依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,即运算循环
,即运算循环![]() 次(第
次(第![]() 次计算结果为
次计算结果为![]() )结束.
)结束.
(1)输入![]() ,结果依次为
,结果依次为![]() 、___________________、
、___________________、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(依次填入循环计算所缺的几次结果)
(2)输入![]() ,运算循环__________次结束.
,运算循环__________次结束.
(3)输入正整数![]() ,经过
,经过![]() 次运算结束,试求
次运算结束,试求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com