
【题目】在直角坐标系中画出一次函数![]() 的图像,并完成下列问题:
的图像,并完成下列问题:
(![]() )此函数图像与坐标轴围成的三角形的面积是______;
)此函数图像与坐标轴围成的三角形的面积是______;
(![]() )观察图像,当
)观察图像,当![]() 时,y的取值范围是______;
时,y的取值范围是______;
(![]() )将直线
)将直线![]() 平移后经过点
平移后经过点![]() ,求平移后的直线的函数表达式.
,求平移后的直线的函数表达式.

【答案】(1)4;( ![]() )
)![]() ;(
;( ![]() )
)![]() .
.
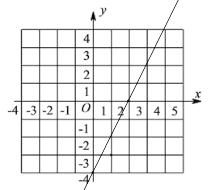
【解析】试题分析:利用“两点确定一条直线”作出函数y=2x-4的图象;
(1)分别求出函数图象与x轴、y轴的交点坐标,再利用三角形的面积公式进行求解即可;
(2)根据图象可知x=0时,y=-4,x=4时,y=4即可得;
(3)设平移后的函数表达式为y=2x+b,将![]() 代入,解得b=7,即可得.
代入,解得b=7,即可得.
试题解析:(1)令y=0,解得x=2,
∴直线与x轴交点坐标为(2,0),与y轴交点坐标为(0,-4),
∴此三角形的面积S=![]() =4,
=4,
故答案为:4;
(![]() )根据图象可知x=0时,y=-4,x=4时,y=4, 所以当
)根据图象可知x=0时,y=-4,x=4时,y=4, 所以当![]() 时,
时, ![]() 的取值范围为
的取值范围为![]() ,
,
故答案为: ![]() ;
;
(![]() )设平移后的函数表达式为y=2x+b,将
)设平移后的函数表达式为y=2x+b,将![]() 代入,解得b=7,
代入,解得b=7,
∴函数解析式为![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离是( )
A. 7cm B. 1cm C. 7cm或4cm D. 7cm或1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
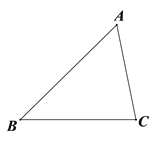
【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下面的解答过程补充完整:
如图,已知EF⊥AB,CD⊥AB,AC⊥BC,![]() ,求证:DG⊥BC
,求证:DG⊥BC

证明:∵ EF⊥AB,CD⊥AB(已知)
∴![]() (___________)
(___________)
∴EF∥CD (_____________________________)
∴![]() ____(_________________________)
____(_________________________)
∵![]() (已知)
(已知)
∴![]() _____(______________________)
_____(______________________)
∴DG∥AC(______________________________)
∴![]() (_____________________________)
(_____________________________)
∵AC⊥BC(已知)
∴ ![]()
∴![]() ,即DG⊥BC
,即DG⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
(1)请在如图所示的网格平面内,作出平面直角坐标系;
(2)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)写出点![]() 的坐标为___ __;
的坐标为___ __;
(4)△ABC的面积为__ _ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若BC=20,DE=12,求△MDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )个
①1乘以任何有理数都等于这个数本身:②0乘以任何数的积均为0:③-1乘以任何有理数都等于这个有理数的相反数;④一个数的倒数与本身相等的数只有1
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为 ,经过61次旋转后,顶点O经过的总路程为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com