
【题目】如图,反比例函数y=![]() 与反比例函数y=k2
与反比例函数y=k2![]() +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与![]() 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=![]() 。
。
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
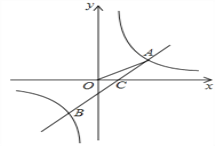
【答案】(1)直线AB的解析式为y=![]() x-1;(2)
x-1;(2)![]() .
.
【解析】试题分析:(1)用待定系数法求函数表达式,需要知道图像上点的坐标,根据![]() ,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入
,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入![]() ,求得反比例函数解析式
,求得反比例函数解析式![]() ,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式
,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式![]() ;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
试题解析:(1)过A作AE⊥x轴于E,∵tan∠AOE=tanα=![]() ,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数
,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数![]() 图像上,∴k1=4,∴反比例函数为
图像上,∴k1=4,∴反比例函数为![]() .∵B(-2,n)在反比例函数
.∵B(-2,n)在反比例函数![]() 图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得:
图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得: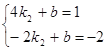 ,解得k2=
,解得k2=![]() ,b="-1," ∴直线AB的解析式为y=
,b="-1," ∴直线AB的解析式为y=![]() x-1;
x-1;
(2)∵直线AB的表达式为y=![]() x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
∴tanβ=![]() =
=![]() .
.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,以点D为中线把正方形ABCD的边DC顺时针旋转α度(0<α<360°)得DE,连接AE、BE.
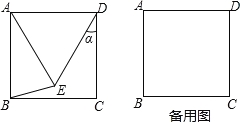
(1)当α=30时,求证:△ABE是等腰三角形;
(2)除30外,当α等于多少时,△ABE是等腰三角形?请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
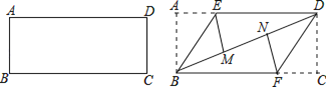
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点横坐标是2,与
图象的顶点横坐标是2,与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0),
,0),![]() ﹤0﹤
﹤0﹤![]() ,与
,与![]() 轴交于点C,
轴交于点C,![]() 为坐标原点,
为坐标原点,![]() .
.
(1)求证:![]() ;
;
(2)求![]() 、
、![]() 的值;
的值;
(3)当![]() ﹥0且二次函数图象与直线
﹥0且二次函数图象与直线![]() 仅有一个交点时,求二次函数的最大值.
仅有一个交点时,求二次函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价为a元,由于供不应求,先提价20%进行销售,后因供应逐步充足,价格又一次性降价20%,售价为b元,则a,b的大小关系为( )
A. b=a B. b=0.96a C. b=a﹣20% D. b=a+20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中不是随机事件的是( )
A.打开电视机正好在播放广告
B.从有黑球和白球的盒子里任意拿出一个正好是白球
C.从课本中任意拿一本书正好拿到数学书
D.明天太阳会从西方升起
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com