
| A. | x1=-1,x2=1 | B. | x1=-1,x2=2 | C. | x1=-2,x2=1 | D. | x1=-2,x2=2 |
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
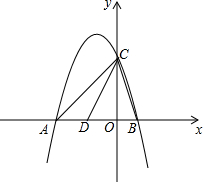 如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 170 | B. | 400 | C. | 1万 | D. | 3万 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
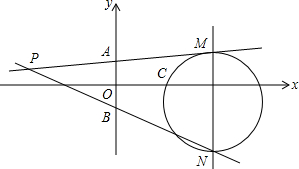 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )
如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )| A. | 12cm | B. | 9cm | C. | 7cm | D. | 15cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com