Question

【题目】二次函数y=+bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A（4，0）和y轴上点C（0，﹣3）．

（1）直接写出b，c，k的值，b=　　，c=　　，k=　　；

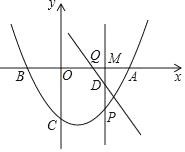
（2）二次函数与x轴的另一个交点为B，点M（m，0）在线段AB上运动，过点M作x轴的垂线交直线AC于点D；交抛物线于点P．

①是否存在实数m，使△PCD为直角三角形．若存在、求出m的值；若不存在，请说明理由；

②当0＜m＜4时，过D作直线AC的垂线交x轴于点Q，求PD+DQ的最大值．

Answer 1

【答案】(1)﹣，﹣3；；（2）①存在，m的值为2或﹣；② ．

【解析】

(1)根据点A、B在二次函数 的图象上，列方程组即可求出b、c的值，把点A代入y=kx﹣3求出k的值即可.（2）①由点M坐标为（m，0）可知点 D、P的坐标分别为D（m， m﹣3），P（m，m2﹣m﹣3），当∠DPC=90°时，CP⊥PD，则m2﹣m﹣3=﹣3，解方程得m=0（舍去）或m=2，当∠PCD=90°，CP⊥CD，

直线PC交x轴于N，如图2，可证明△AMD∽△AOC，得OC2=ONOA，所以 ON= 可知点N坐标为（﹣，0），得直线CN的解析式为y=﹣x﹣3，列方程组求出P点坐标，即可得m的值.，②由可知OC=3，OA=4，AC=5，因为DM∥OC，所以△AMD∽△AOC，得 ，AM=4-m，所以AD= -m+5，由DQ⊥AC，可证明△ADQ∽△AOC，所以 ，得DQ=﹣m+，因为DP=m﹣3﹣（m2﹣m﹣3），=﹣m2+m，所以PQ+DQ=+，

当m=时，PQ+DQ有最大值，

（1）把A（4，0），C（0，﹣3）代入y= +bx+c得解得 ，

∴抛物线解析式为y= ﹣x﹣3；

把A（4，0）代入y=kx﹣3得4k﹣3=0，解得k=，

直线AC的解析式为y=x﹣3；

故答案为﹣，﹣3；

（2）①存在．

M（m，0），则D（m， m﹣3），P（m，m2﹣m﹣3），

当∠DPC=90°时，CP⊥PD，则m2﹣m﹣3=﹣3，解得，m1=0（舍去），m2=2；

当∠PCD=90°，CP⊥CD，

直线PC交x轴于N，如图2，

易得△CON∽△AOC，

∴OC2=ONOA，

∴ON=，则N（﹣，0），

易得直线CN的解析式为y=﹣ x﹣3，

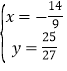解方程组得 或 ，则P（﹣，﹣ ），

综上所述，m的值为2或﹣；

②M（m，0），则D（m， m﹣3），P（m，m2﹣m﹣3），

∵OC=3，OA=4，

∴AC=5，

∵DM∥OC，

∴△AMD∽△AOC，

∴ ，即 ，解得AD=﹣m+5，

∵DQ⊥AC，

∴△ADQ∽△AOC，

∴，即= ，解得DQ=﹣m+，

而DP=m﹣3﹣（m2﹣m﹣3）=﹣m2+m，

∴DP+DQ=﹣m2+m﹣m+=﹣m2+m+=﹣（m﹣）2+，

当m=时，PD+DQ有最大值为．