
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处(点C在∠AOB的内部或一边上).
(1)当PC∥QB时,OQ= cm.
(2)当折叠后重叠部分为等腰三角形时,画出示意图,写出OQ的长.

【答案】(1)2;(2)画图见解析,OQ的长为2cm或![]() cm或2
cm或2![]() cm.
cm.
【解析】
(1)由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有3个;依据点C在∠AOB的内部或一边上,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长.
(1)当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2;
(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ.
因为△CPQ是由△OPQ折叠得到,所以当△OPQ为等腰三角形时,重叠部分必为等腰三角形.
分三种情况:
①当PQ=PO时,OQ=![]() OP=2
OP=2![]() cm,
cm,

②当QO=QP时,OQ=![]() OP=
OP=![]() cm,
cm,
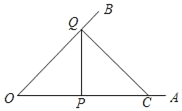
③当OQ=OP时,OQ=OP=2cm.
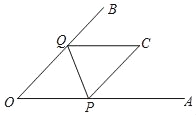
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或![]() cm或2
cm或2![]() cm.
cm.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中![]() 表示小强从家出发后的时间,
表示小强从家出发后的时间,![]() 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量![]() 与
与![]() 之间关系的大致图象是( )
之间关系的大致图象是( )
A.  B.
B. 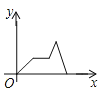
C.  D.
D. 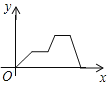
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积.
(2)若连接AD、CF,则这两条线段之间的关系是 ;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:

尺规作图:
已知:线段a,b.
求作:等腰△ABC,使AB=AC,BC=a,BC边上的高为b.
小涛的作图步骤如下:
如图
(1)作线段BC=a;
(2)作线段BC的垂直平分线MN交线段BC
于点D;
(3)在MN上截取线段DA=b,连接AB,AC.
所以△ABC即为所求作的等腰三角形.
老师说:“小涛的作图步骤正确”.
请回答:得到△ABC是等腰三角形的依据是:
①_____;
②_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n-![]() ≤x<n+
≤x<n+![]() ,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若(
,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若(![]() x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号)
x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com