
ΓΨΧβΡΩΓΩ‘ΡΕΝ”κ”Π”ΟΘΚ‘ΡΕΝ1ΘΚaΓΔbΈΣ Β ΐΘ§«“aΘΨ0Θ§bΘΨ0Θ§“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() ¥”Εχ
¥”Εχ![]() Θ®Β±a=b ±»ΓΒ»Κ≈Θ©Θ°
Θ®Β±a=b ±»ΓΒ»Κ≈Θ©Θ°
‘ΡΕΝ2ΘΚ»τΚ· ΐ![]() ΘΜΘ®mΘΨ0Θ§xΘΨ0Θ§mΈΣ≥Θ ΐΘ©Θ§”…‘ΡΕΝ1Ϋα¬έΩ…÷ΣΘΚ
ΘΜΘ®mΘΨ0Θ§xΘΨ0Θ§mΈΣ≥Θ ΐΘ©Θ§”…‘ΡΕΝ1Ϋα¬έΩ…÷ΣΘΚ![]() Θ§Υυ“‘Β±
Θ§Υυ“‘Β±![]() Θ§Φ¥
Θ§Φ¥![]() ±Θ§Κ· ΐ
±Θ§Κ· ΐ![]() ΒΡΉν–Γ÷ΒΈΣ
ΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°
‘ΡΕΝάμΫβ…œ ωΡΎ»ίΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Έ Χβ1ΘΚ“―÷Σ“ΜΗωΨΊ–ΈΒΡΟφΜΐΈΣ4Θ§Τδ÷–“Μ±Ώ≥ΛΈΣxΘ§‘ρΝμ“Μ±Ώ≥ΛΈΣ![]() Θ§÷ή≥ΛΈΣ2Θ®
Θ§÷ή≥ΛΈΣ2Θ®![]() Θ©Θ§«σΒ±x= ±Θ§÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ ΘΜ
Θ©Θ§«σΒ±x= ±Θ§÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ ΘΜ
Έ Χβ2ΘΚ“―÷ΣΚ· ΐ![]() Θ®
Θ®![]() Θ©”κΚ· ΐ
Θ©”κΚ· ΐ![]() Θ®
Θ®![]() Θ©Θ§
Θ©Θ§
Β±x= ±Θ§![]() ΒΡΉν–Γ÷ΒΈΣ ΘΜ
ΒΡΉν–Γ÷ΒΈΣ ΘΜ
Έ Χβ3ΘΚΡ≥ΟώΑλ―ß–ΘΟΩΧλΒΡ÷ß≥ωΉήΖ―”ΟΑϋΚ§“‘œ¬»ΐΗω≤ΩΖ÷ΘΚ“Μ «ΫΧ÷ΑΙΛΙΛΉ 4900‘ΣΘΜΕΰ «―ß…ζ…ζΜνΖ―≥…±ΨΟΩ»Υ10‘ΣΘΜ»ΐ «ΤδΥϊΖ―”ΟΘ°Τδ÷–Θ§ΤδΥϊΖ―”Ο”κ―ß…ζ»Υ ΐΒΡΤΫΖΫ≥…’ΐ±»Θ§±»άΐœΒ ΐΈΣ0.01Θ°Β±―ß–Θ―ß…ζ»Υ ΐΈΣΕύ…Ό ±Θ§ΗΟ–ΘΟΩΧλ…ζΨυΆΕ»κΉνΒΆΘΩΉνΒΆΖ―”Ο «Εύ…Ό‘ΣΘΩΘ®…ζΨυΆΕ»κ=÷ß≥ωΉήΖ―”ΟΓ¬―ß…ζ»Υ ΐΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©2Θ§8ΘΜΘ®2Θ©2Θ§6ΘΜΘ®3Θ©700Θ§24Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΈ Χβ1ΘΚ”…‘ΡΕΝ2ΒΟΒΫ![]() ΒΡΖΕΈßΘ§Ϋχ“Μ≤ΫΒΟΒΫ÷ή≥ΛΒΡΉν–Γ÷ΒΘΜ
ΒΡΖΕΈßΘ§Ϋχ“Μ≤ΫΒΟΒΫ÷ή≥ΛΒΡΉν–Γ÷ΒΘΜ
Έ Χβ2ΘΚΑ―![]() ±δ–ΈΈΣ
±δ–ΈΈΣ![]() Θ§”…‘ΡΕΝ2ΒΟΒΫ
Θ§”…‘ΡΕΝ2ΒΟΒΫ![]() ΒΡΖΕΈßΘ§Ϋχ“Μ≤ΫΦ¥Ω…«σΫβΘΜ
ΒΡΖΕΈßΘ§Ϋχ“Μ≤ΫΦ¥Ω…«σΫβΘΜ
Έ Χβ3ΘΚΩ……η―ß–Θ―ß…ζ»Υ ΐΈΣx»ΥΘ§ΗυΨί…ζΨυΆΕ»κ=÷ß≥ωΉήΖ―”ΟΓ¬―ß…ζ»Υ ΐΘ§Ν–≥ω¥ζ ΐ ΫΘ§‘Ό”…‘ΡΕΝ2ΒΟΒΫΖΕΈßΘ§¥”Εχ«σΫβΘ°
‘ΧβΫβΈωΘΚΈ Χβ1ΘΚ![]() Θ®
Θ®![]() Θ©Θ§ΫβΒΟx=2Θ§x=2 ±Θ§
Θ©Θ§ΫβΒΟx=2Θ§x=2 ±Θ§![]() ”–Ήν–Γ÷ΒΈΣ
”–Ήν–Γ÷ΒΈΣ![]() =4Θ°Ι Β±x=2 ±Θ§÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ2ΓΝ4=8ΘΜ
=4Θ°Ι Β±x=2 ±Θ§÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ2ΓΝ4=8ΘΜ
Έ Χβ2ΘΚΓΏ![]() Θ®
Θ®![]() Θ©Θ§
Θ©Θ§![]() Θ®
Θ®![]() Θ©Θ§Γύ
Θ©Θ§Γύ![]() =
=![]() Θ§
Θ§![]() Θ§ΫβΒΟx=2Θ§x=2 ±Θ§
Θ§ΫβΒΟx=2Θ§x=2 ±Θ§![]() ”–Ήν–Γ÷ΒΈΣ
”–Ήν–Γ÷ΒΈΣ![]() =6ΘΜ
=6ΘΜ
Έ Χβ3ΘΚ…η―ß–Θ―ß…ζ»Υ ΐΈΣx»ΥΘ§‘ρ…ζΨυΆΕ»κ=![]() =
=![]() =
=![]() Θ§
Θ§![]() Θ®
Θ®![]() Θ©Θ§ΫβΒΟx=700Θ§x=700 ±Θ§
Θ©Θ§ΫβΒΟx=700Θ§x=700 ±Θ§![]() ”–Ήν–Γ÷ΒΈΣ
”–Ήν–Γ÷ΒΈΣ![]() =1400Θ§Ι Β±x=700 ±Θ§…ζΨυΆΕ»κΒΡΉν–Γ÷ΒΈΣ10+0.01ΓΝ1400=24‘ΣΘ°
=1400Θ§Ι Β±x=700 ±Θ§…ζΨυΆΕ»κΒΡΉν–Γ÷ΒΈΣ10+0.01ΓΝ1400=24‘ΣΘ°
¥πΘΚΒ±―ß–Θ―ß…ζ»Υ ΐΈΣ700 ±Θ§ΗΟ–ΘΟΩΧλ…ζΨυΆΕ»κΉνΒΆΘ§ΉνΒΆΖ―”Ο «24‘ΣΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΓΈCDΘ§ΒψEΘ§FΖ÷±π‘ΎABΘ§CD…œΘ§Ν§Ϋ”EFΘ§ΓœAEFΓΔΓœCFEΒΡΤΫΖ÷œΏΫΜ”ΎΒψGΘ§ΓœBEFΓΔΓœDFEΒΡΤΫΖ÷œΏΫΜ”ΎΒψHΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈEGFH «ΨΊ–ΈΘΜ
Θ®2Θ©–ΓΟς‘ΎΆξ≥…Θ®1Θ©ΒΡ÷ΛΟςΚσΦΧ–χΫχ––ΝΥΧΫΥςΘ§ΙΐGΉςMNΓΈEFΘ§Ζ÷±πΫΜABΘ§CD”ΎΒψMΘ§NΘ§ΙΐHΉςPQΓΈEFΘ§Ζ÷±πΫΜABΘ§CD”ΎΒψPΘ§QΘ§ΒΟΒΫΥΡ±Ώ–ΈMNQPΘ§¥Υ ±Θ§Υϊ≤¬œκΥΡ±Ώ–ΈMNQP «Νβ–ΈΘ§«κ‘Ύœ¬Ν–Ωρ÷–≤Ι»ΪΥϊΒΡ÷ΛΟςΥΦ¬ΖΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣxΘΫ2 «“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ®m©¹2Θ©x2+4x©¹m2ΘΫ0ΒΡ“ΜΗωΗυΘ§‘ρmΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
A.2B.0Μρ2C.0Μρ4D.0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“Μ¥ΈΚ· ΐy= -2x+4ΒΡΆΦœσ”κΉχ±ξ÷αΥυΈß≥…ΒΡ»ΐΫ«–ΈΟφΜΐ « _____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβ≈ΉΈοœΏ![]() …œ»Έ“β“ΜΒψΒΫΒψΘ®0Θ§1Θ©ΒΡΨύάκ”κΒΫ÷±œΏy=©¹1ΒΡΨύάκœύΒ»Θ§ΡψΩ…“‘άϊ”Ο’β“Μ–‘÷ ΫβΨωΈ ΧβΘ°
…œ»Έ“β“ΜΒψΒΫΒψΘ®0Θ§1Θ©ΒΡΨύάκ”κΒΫ÷±œΏy=©¹1ΒΡΨύάκœύΒ»Θ§ΡψΩ…“‘άϊ”Ο’β“Μ–‘÷ ΫβΨωΈ ΧβΘ°
Έ ΧβΫβΨω
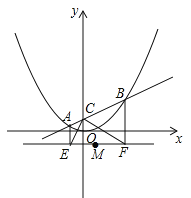
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏ![]() ”κy÷αΫΜ”ΎCΒψΘ§”κΚ· ΐ
”κy÷αΫΜ”ΎCΒψΘ§”κΚ· ΐ![]() ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§Ζ÷±πΙΐAΘ§BΝΫΒψΉς÷±œΏy=©¹1ΒΡ¥ΙœΏΘ§ΫΜ”ΎEΘ§FΝΫΒψΘ°
ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§Ζ÷±πΙΐAΘ§BΝΫΒψΉς÷±œΏy=©¹1ΒΡ¥ΙœΏΘ§ΫΜ”ΎEΘ§FΝΫΒψΘ°
Θ®1Θ©–¥≥ωΒψCΒΡΉχ±ξΘ§≤ΔΥΒΟςΓœECF=90ΓψΘΜ
Θ®2Θ©‘ΎΓςPEF÷–Θ§MΈΣEF÷–ΒψΘ§PΈΣΕ·ΒψΘ°
ΔΌ«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
ΔΎ“―÷ΣPE=PF=3Θ§“‘EFΈΣ“ΜΧθΕ‘Ϋ«œΏΉςΤΫ––ΥΡ±Ώ–ΈCEDFΘ§»τ1ΘΦPDΘΦ2Θ§ ‘«σCPΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΒψP(aΘ§b)‘ΎΒΎΕΰœσœόΘ§‘ρΒψM(bΘ≠aΘ§aΘ≠b)‘Ύ( )
A. ΒΎ“Μœσœό B. ΒΎΕΰœσœό C. ΒΎ»ΐœσœό D. ΒΎΥΡœσœό
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘≤ΉΕΒΡΒΉΟφΑκΨΕΈΣ5Θ§ΗΏΈΣ12Θ§‘ρΥϋΒΡ≤ύΟφΜΐΈΣ_______
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“εΘΚ»γΆΦ1Θ§ΒψMΘ§NΑ―œΏΕΈABΖ÷Ην≥…AMΘ§MNΚΆBNΘ§»τ“‘AMΘ§MNΘ§BNΈΣ±ΏΒΡ»ΐΫ«–Έ «“ΜΗω÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ≥ΤΒψMΘ§N «œΏΕΈABΒΡΙ¥Ι…Ζ÷ΗνΒψΘ°
Θ®1Θ©“―÷ΣΒψMΘ§N «œΏΕΈABΒΡΙ¥Ι…Ζ÷ΗνΒψΘ§»τAM=2Θ§MN=3Θ§«σBNΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦ2Θ§‘ΎΓςABC÷–Θ§FG «÷–ΈΜœΏΘ§ΒψDΘ§E «œΏΕΈBCΒΡΙ¥Ι…Ζ÷ΗνΒψΘ§«“ECΘΨDEΓίBDΘ§Ν§Ϋ”ADΘ§AEΖ÷±πΫΜFG”ΎΒψMΘ§NΘ§«σ÷ΛΘΚΒψMΘ§N «œΏΕΈFGΒΡΙ¥Ι…Ζ÷ΗνΒψΘΜ
Θ®3Θ©“―÷ΣΒψC «œΏΕΈAB…œΒΡ“ΜΕ®ΒψΘ§ΤδΈΜ÷Ο»γΆΦ3Υυ ΨΘ§«κ‘ΎBC…œΜ≠“ΜΒψDΘ§ ΙΒψCΘ§D «œΏΕΈABΒΡΙ¥Ι…Ζ÷ΗνΒψΘ®“Σ«σ≥ΏΙφΉςΆΦΘ§±ΘΝτΉςΆΦΚέΦΘΘ§Μ≠“Μ÷÷«ι–ΈΦ¥Ω…Θ©ΘΜ
Θ®4Θ©»γΆΦ4Θ§“―÷ΣΒψMΘ§N «œΏΕΈABΒΡΙ¥Ι…Ζ÷ΗνΒψΘ§MNΘΨAMΓίBNΘ§ΓςAMCΘ§ΓςMNDΚΆΓςNBEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§AEΖ÷±πΫΜCMΘ§DMΘ§DN”ΎΒψFΘ§GΘ§HΘ§»τH «DNΒΡ÷–ΒψΘ§ ‘ΧΫΨΩ![]() Θ§
Θ§![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com