
【题目】如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如(1,0),(2,0)(2,1),(3,2),(3,1)(3,0),……,根据这个规律探索可得,第102个点的坐标为______________;

科目:初中数学 来源: 题型:
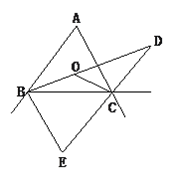
【题目】如图所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
【题目】乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.

![]()
(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
![]() =________;
=________; ![]() =________.
=________.
拓展运用:
(5)计算: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的是______________;
① xy +2x -y =7 ;② 4x+1=x-y ;③![]() +y=5 ;④ x=y ;⑤ x2-y2=2
+y=5 ;④ x=y ;⑤ x2-y2=2
⑥ 6x-2y ;⑦ x+y+z=1 ;⑧ y(y-1)=2y2-y2+x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-2,0),B(0,3),O 为原点.
(1)求三角线 AOB 的面积;
(2)将线段 AB 沿 x 轴向右平移4个单位,得线段A′B′,x轴上有一点C满足三角形A′B′C的面积为 9 ,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这1000名考生是总体的一个样本
B.近4万名考生是总体
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC和等腰△ACD有一条公共边AC,且顶角∠BAC和顶角∠CAD都是45°.将一块三角板中用含45°角的顶点与A点重合,并将三角板绕A点按逆时针方向旋转.
(1)当三角板旋转到如图1的位置时,三角板的两边与等腰三角形的两底边分别相交于M、N两点,求证:AM=AN;
(2)当三角板旋转到如图2的位置时,三角板的两边与等腰三角形两底边的延长线分别相交于M、N两点,(1)的结论还成立吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com