
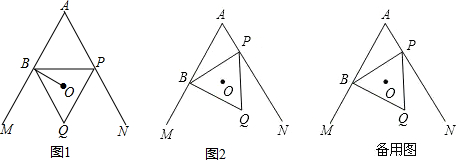
分析 (1)先求得∠BOP=120°,在四边形ABOP中依据四边形的内角和是360°可求得∠APO的度数,然后依据角平分线的逆定理证明即可;
(2)连接OB、OP、OA,由∠A=60°,∠BOP=120°,可证明A、B、O、P四点共圆,然后依据同圆和等圆中相等的弦所对的圆周角相等可得到∠BAO=∠PAO;
(3)连接OB、OP、AO.先证明△ABO∽△ACP,由相似三角形的性质可知AC•AO=AB•PA,从而可求得答案;
(4)如图4所示:当点P与点D重合时.先证明三角形AOB为直角三角形,然后依据特殊锐角三角函数值可求得AO的长;如图5所示:当点A与点P重合时.先证明△AOD为直角三角形,然后依据特殊锐角三角函数值可求得AO的长;如图6所示:证明∠OBD=∠ABD=30°,从而得到点A与点O重合.
解答 解:(1)在.
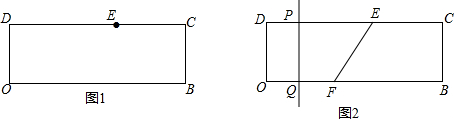
理由:如图1所示:连接OP.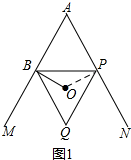
∵点O为等边△BQP的外心,
∴∠BOP=2∠BQP=120°,OB=OP.
∵OB⊥AM,
∴∠ABO=90°.
∵∠A+∠ABO+∠BOP+∠OPA=180°,
∴∠OPA=90°.
∴OP⊥AN.
∵OP=OB,OP⊥AN,OB⊥AM,
∴点O在∠MAN的平分线上.
(2)当点A与点P不重合时,如图2所示:连接OB、OP、OA.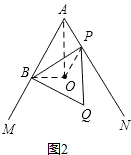
∵点O是等边三角形BOQ的外心,
∴∠BOP=120°,OP=OB.
∵∠BAP=60°,
∴∠BAP+∠BOP=180°.
∴点A、B、O、P共圆.
又∵OB=OP,
∴∠BAO=∠PAO.
∴点O在MAN的角平分线上.
当点P与点A重合时.
∵点O是等边三角形BOQ的外心,
∴PO平分∠BPQ.
∵∠BPQ与∠MAN重合,
∴∠PO平分∠MAN.
综上所示,总有点O在∠MAN的平分线.
(3)如图3所示:连接OB、OP、AO.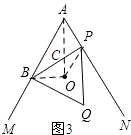
∵由(2)可知点B、O、P、A共圆,
∴∠BOA=∠BPA.
∵AO平分∠MAN,
∴∠BAO=∠PAO.
∴△ABO∽△ACP.
∴$\frac{AB}{AC}=\frac{AO}{AP}$.
∴AC•AO=AB•PA.
∴AC•AO=4m.
(4)如图4所示:当点P与点D重合时.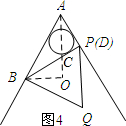
∵∠BAP=60°,BA=4,AD=2,
∴BP⊥AP.
∴∠BPA=90°.
又∵∠PAC=$\frac{1}{2}$∠MAN=30°,
∴∠OCB=∠ACP=60°.
∵O为等边三角形的外心,
∴∠OBC=30°.
∴∠BOC=90°.
在Rt△AOB中,OA=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$.
如图5所示:当点A与点P重合时.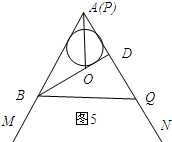
∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AQ.
∴∠BDA=90°.
∵在Rt△AOD中,∠DAO=30°,AD=2,
∴AO=AD÷$\frac{\sqrt{3}}{2}$=2×$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
如图6所示: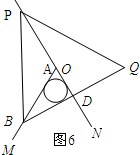
∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AN.
∴∠BDA=90°.
∴∠ABD=30°
∵O为△BPQ的外心,
∴∠OBD=30°.
∴点A与点O重合.
∴OA=0.
综上所述,OA=2$\sqrt{3}$或OA=$\frac{4\sqrt{3}}{3}$或AO=0.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了相似三角形的性质和判定、四点共圆、角平分线的判定定理、三角形的外心的性质、圆周角定理的,画出符合题意的图形,并恰当作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G.
如图,在?ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com