
分析 利用三角函数求出∠AOD=45°,再根据等腰三角形三线合一得:∠AOB=90°,即中心角为90°,利用周角计算边的数:n=360÷90=4.
解答 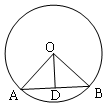 解:如图所示,半径OA=OB=4,边心距OD⊥AB,且OD=2$\sqrt{2}$,
解:如图所示,半径OA=OB=4,边心距OD⊥AB,且OD=2$\sqrt{2}$,
在Rt△AOD中,cos∠AOD=$\frac{OD}{AO}$=$\frac{2\sqrt{2}}{4}$=$\frac{\sqrt{2}}{2}$,
∴∠AOD=45°,
∵OA=OB,OD⊥AB,
∴∠BOD=∠AOD=45°,
∴∠AOB=90°,
∴n=$\frac{360°}{90°}$=4;
故答案为:4.
点评 本题考查了正多边形和圆的定义,明确正n边形的外接圆半径与边构成n个等腰三角形,其边心距就是等腰三角形底边上的高,利用勾股定理或三角函数可计算边或角的值.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.| A. | 10°和40° | B. | 10°和50° | C. | 40°和50° | D. | 10°和60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
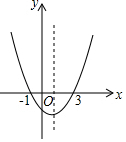 已知y=ax2+bx+c的图象如图所示,在下列说法中:①ac<0;②3a+c=0;③4a+2b+c>0;④当x>1时,y随着x的增大而增大;⑤2a+b=0;⑥a+b+c=0.其中正确的有( )
已知y=ax2+bx+c的图象如图所示,在下列说法中:①ac<0;②3a+c=0;③4a+2b+c>0;④当x>1时,y随着x的增大而增大;⑤2a+b=0;⑥a+b+c=0.其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知在直角坐标系中,点P是直线y=-x+4上的一个动点,⊙O的半径为1,过点P作⊙O的切线,切点为A,则PA长度的最小值为$\sqrt{7}$.
如图,已知在直角坐标系中,点P是直线y=-x+4上的一个动点,⊙O的半径为1,过点P作⊙O的切线,切点为A,则PA长度的最小值为$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.295≤a<2.305 | B. | 2.25≤a<2.35 | C. | 2.295≤a≤2.305 | D. | 2.25<a≤2.35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com