
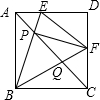
 如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论
如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论| A. | 只有①②③ | B. | 只有②④ | C. | 只有①③④ | D. | ①②③④ |
分析 过P点作MN⊥AB,交DC于M,交AB于N,作PH⊥AD于H,由正方形的性质得AB=AD,AN=AH,则BN=HD,而HD=PM,所以BN=PM,接着证明△BPN≌△PFM得到PB=FB,于是可判断△PBF为等腰直角三角形,所以∠PBF=45°,则可对①进行判断;延长DC到E′,使CE′=AE,连结BE′,如图,先证明△ABE≌△CBE′得到BE=BE′,∠ABE=∠CBE′,再证明∠E′BF=45°,则可根据“SAS”判断△BEF≌△BE′F,得到EF=E′F,则EF=AE+FC,利用等线段代换可得△DEF的周长=AD+DC=8,则可对②进行判断;在BE′截取BP′=BP,连结CP′,QP′,易证得△BAP≌△BCP′,得到∠BAP=∠BCP′=45°,AP=CP′,所以∠QCP′=90°,然后证明△BPQ≌△BP′Q得到PQ=P′Q,再在Rt△QCP′中根据勾股定理得CP′2+CQ2=P′Q2,利用等线段代换即可得到AP2+CQ2=PQ2,则可对③进行判断;在Rt△BFC中,利用勾股定理计算出BF=2$\sqrt{5}$,然后根据△PBF为等腰直角三角形可得PF=$\frac{\sqrt{2}}{2}$BF=$\sqrt{10}$,于是可对④进行判断.
解答 解:过P点作MN⊥AB,交DC于M,交AB于N,作PH⊥AD于H,如图1,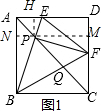
∵四边形ABCD为正方形,
∴AB=AD,AN=AH,
∴BN=HD,
而HD=PM,
∴BN=PM,
∵PF⊥PB,
∴∠BPF=90°,
∴∠BPN+∠FPM=90°,
而∠BPN+∠PBN=90°,
∴∠PBN=∠FPM,
在△BPN和△PFM中
$\left\{\begin{array}{l}{∠PNB=∠FMP}\\{BN=PM}\\{∠PBN=∠FPM}\end{array}\right.$,
∴△BPN≌△PFM,
∴PB=FB
∴△PBF为等腰直角三角形,
∴∠PBF=45°,所以①正确;
延长DC到E′,使CE′=AE,连结BE′,如图2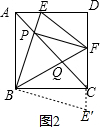 ,
,
在△ABE和△CBE′中,
$\left\{\begin{array}{l}{AB=CB}\\{∠BAE=∠BCE′}\\{AE=CE′}\end{array}\right.$,
∴△ABE≌△CBE′,
∴BE=BE′,∠ABE=∠CBE′,
∴∠EBE′=∠EBC+∠CBE′=∠EBC+∠ABE=∠ABC=90°,
而∠EBF=45°,
∴∠E′BF=45°,
在△BEF和△BE′F中
$\left\{\begin{array}{l}{BE=BE′}\\{∠EBF=∠E′BF}\\{BF=BF}\end{array}\right.$,
∴△BEF≌△BE′F,
∴EF=E′F,
而E′F=FC+CE′=FC+AE,
∴EF=AE+FC,
∴△DEF的周长=DE+DF+EF=DE+DF+AE+FC=AD+DC=4+4=8,所以②正确;
在BE′截取BP′=BP,连结CP′,QP′,如图3,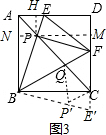
在△BAP和△BCP′中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABP=∠CBP′}\\{BP=BP′}\end{array}\right.$,
∴△BAP≌△BCP′,
∴∠BAP=∠BCP′=45°,AP=CP′,
而∠ACB=45°,
∴∠QCP′=90°,
在△BPQ和△BP′Q中
$\left\{\begin{array}{l}{BP=BP′}\\{∠PBQ=∠P′BQ}\\{BQ=BQ}\end{array}\right.$,
∴△BPQ≌△BP′Q,
∴PQ=P′Q,
在Rt△QCP′中,CP′2+CQ2=P′Q2,
∴AP2+CQ2=PQ2,所以③正确;
∵F为CD的中点,
∴FC=2,
在Rt△BFC中,BF=$\sqrt{F{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵△PBF为等腰直角三角形,
∴PF=$\frac{\sqrt{2}}{2}$BF=$\frac{\sqrt{2}}{2}$×2$\sqrt{5}$=$\sqrt{10}$,所以④正确.
故选D.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了全等三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | 如果a∥b,a⊥c,那么b⊥c | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 如果b⊥a,c⊥a,那么b⊥c | D. | 如果b⊥a,c⊥a,那么b∥c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com