
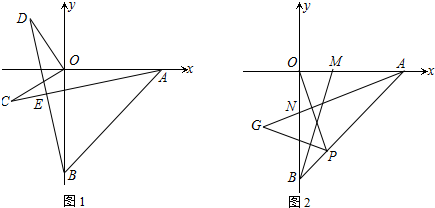
分析 (1)根据非负数的性质得出a=5,b=-5即可;
(2)过C作CK⊥x轴,过D作CF⊥y轴,再利用AAS证明△AOC与△DOB全等即可;
(3)延长GP到L使PL=OP,连接AL,证明△PAL与△OAP全等,再利用全等三角形的性质解答即可.
解答 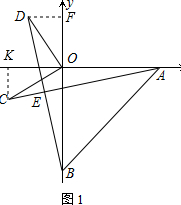 解:(1)∵|a+b|+(a-5)2=0,
解:(1)∵|a+b|+(a-5)2=0,
∴a=5,b=-5,
∴点A的坐标为(5,0),点B的坐标为
(0,-5),
故答案为:(5,0);(0,-5);
(2)过C作CK⊥x轴,过D作DF⊥y轴,
∵∠AED=∠BOK=90°,
∴∠DBO=∠OAC,
∵∠AOB+?BOC=∠BOK+∠BOC=90°+∠BOC,
∴∠AOC=∠BOD,
在△AOC与△DOB中,
$\left\{\begin{array}{l}{∠AOC=∠BOD}\\{∠DBO=∠OAC}\\{OA=OB}\end{array}\right.$,
∴△AOC≌△DOB(AAS),
∴OC=OD,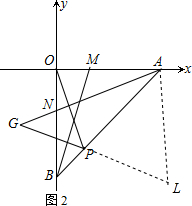
在△OCK与△ODF中,
$\left\{\begin{array}{l}{∠DFO=∠CKO=90°}\\{∠DOF=∠COK}\\{OD=OC}\end{array}\right.$,
∴△OCK≌△ODF,
∴DF=CK,OK=OF,
∴D(-2,3);
(3)延长GP到L,使PL=OP,连接AL,
在△AON与△BOM中,
$\left\{\begin{array}{l}{ON=OM}\\{∠AON=∠BOM}\\{OA=OB}\end{array}\right.$,
∴△AON≌△BOM,
∴∠OAN=∠OBM,
∴∠MBA=∠NAB,
∵PG⊥BM,OP⊥AN,
∴∠NAB+∠OPA=∠MBA+∠GPB=90°,
∴∠OPA=∠GPB=∠APL,
在△OAP与△PAL中,
$\left\{\begin{array}{l}{PL=OP}\\{∠APL=∠OPA}\\{AP=AP}\end{array}\right.$,
∴△OAP≌△PAL,
∴∠POA=∠L,∠OAP=∠PAL=45°,
∴∠OAL=90°,
∴∠POA=90°-∠POB,∠GAL=90°-∠OAN,
∵∠POB=∠OAN,
∴∠POA=∠GOL,
∴∠POA=∠GOL=∠L,
∴AG=GL,
∴AG=GL=GP+PL=GP+OP.
点评 本题考查了全等三角形的性质和判定,平行线的性质的应用,能综合运用定理进行推理是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | a(1-8%)(1+12%)元 | B. | a(1-8%)(1+12%)2元 | C. | (a-8%)(a+12%)元 | D. | a(1-8%+12%)元 |
查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:解答题
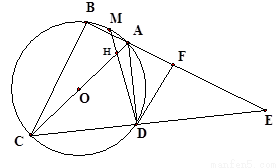
如图,⊙O是四边形ABCD的外接圆,AC是直径,分别延长AB、CD相交于点E,AC=AE,过点D作DF∥BC于点F.
求证:(1)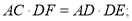
(2)求证:DF是⊙O的切线;
(3)若M是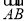 的中点,连接MD交弦AB于点H,若
的中点,连接MD交弦AB于点H,若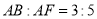 ,证明:
,证明: 
查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:单选题
有五只灯泡,其中两只是次品,从中任取一只恰为合格品的概率为( )
A. 20% B. 40% C. 50% D. 60%
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连接BF交AC、DC、DE分别为P、Q、R.
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连接BF交AC、DC、DE分别为P、Q、R.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
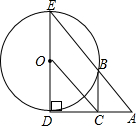 如图.己知DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,连接BC.
如图.己知DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
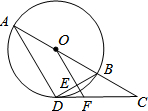 如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.
如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com