
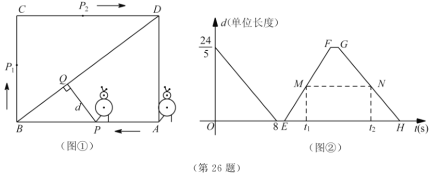
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点![]() 出发,在矩形
出发,在矩形![]() 边上沿着
边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为![]() 个单位长度/
个单位长度/![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要![]()
![]() (即在
(即在![]() 、
、![]() 处拐弯时分别用时
处拐弯时分别用时![]()
![]() ).设机器人所用时间为
).设机器人所用时间为![]() 时,其所在位置用点
时,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)求![]() 、
、![]() 的长;
的长;
(2)如图②,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,线段
上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设机器人用了
.设机器人用了![]() 到达点
到达点![]() 处,用了
处,用了![]() 到达点
到达点![]() 处(见图①).若
处(见图①).若![]() ,求
,求![]() 、
、![]() 的值.
的值.
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】在锐角三角形中,∠A>∠B>∠C,则下列结论中错误的是( )
A. ∠A>60° B. ∠B>45° C. ∠C<60° D. ∠B+∠C<90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
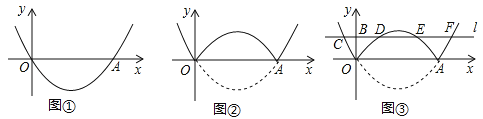
【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣![]() 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.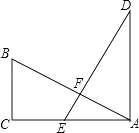
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系XOY中,A(-1,5),B(-1,0),C(-4,3).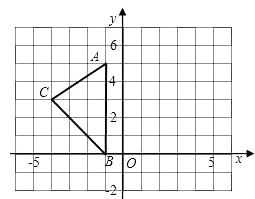
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
(1)按要求作图:
①△ABC关于x轴对称的图形△ ![]() ;
;
②将△ ![]() 向右平移6个单位得到△
向右平移6个单位得到△ ![]() .
.
(2)回答下列问题:
①△ ![]() 中顶点B2坐标为 .
中顶点B2坐标为 .
②若 ![]() 为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com