
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.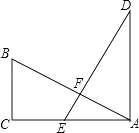
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
【答案】
(1)解:AB=DE, AB⊥DE.
如图2,
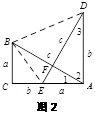
∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE
(2)解:如图2,

∵S四边形ADBE= S△ADE+ S△BDE= ![]() DE·AF+
DE·AF+ ![]() DE·BF=
DE·BF= ![]() DE·AB =
DE·AB = ![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB= ![]() a2+
a2+ ![]() b2,
b2,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.
【解析】(1)由题目中的已知条件可直接得到△ABC≌△DEA,问题得解;(2)四边形ADBE的两种构成:S四边形ADBE= S△ADE+ S△BDE和
S四边形ADBE=S△ABE+S△ADB,可验证勾股定理。


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )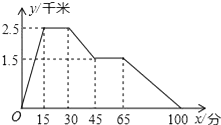
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
D.张强从早餐店回家的平均速度是 ![]() 千米/小时
千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.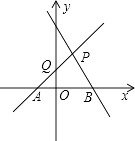
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两直线平行,同旁内角相等B.两直线平行,同位角相等
C.两直线被第三条直线所截,内错角相等D.若一个角的两边分别与另一个角的两边平行,则这两个角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
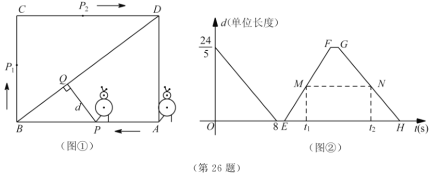
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点![]() 出发,在矩形
出发,在矩形![]() 边上沿着
边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为![]() 个单位长度/
个单位长度/![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要![]()
![]() (即在
(即在![]() 、
、![]() 处拐弯时分别用时
处拐弯时分别用时![]()
![]() ).设机器人所用时间为
).设机器人所用时间为![]() 时,其所在位置用点
时,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)求![]() 、
、![]() 的长;
的长;
(2)如图②,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,线段
上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设机器人用了
.设机器人用了![]() 到达点
到达点![]() 处,用了
处,用了![]() 到达点
到达点![]() 处(见图①).若
处(见图①).若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com