
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.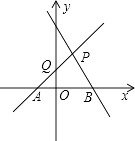
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
【答案】
(1)解:∵一次函数y=x+1的图象与x轴交于点A,∴A(﹣1,0),
一次函数y=﹣2x+2的图象与x轴交于点B,∴B(1,0),
由 ![]() ,解得
,解得 ![]() ,∴P(
,∴P( ![]() ,
, ![]() ).
).
(2)解:设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM﹣S△QPM= ![]() ×1×2﹣
×1×2﹣ ![]() ×1×
×1× ![]() =
= ![]()
【解析】(1)两条直线与x轴相交,y为0,得出两个一元一次方程,求出x的值,则可写出A、B两点的坐标,p为两条直线的交点,解这个二元一次方程组,可得p点的坐标。
(2)设直线PB与y轴交于M点。四边形PQOB的构成是由三角形BOM-三角形PQM得到的。


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.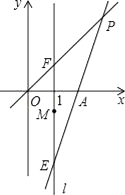
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
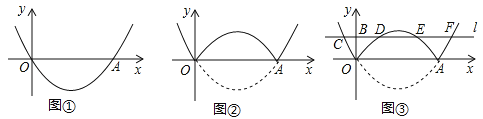
【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣![]() 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份销售额人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 7.2 | 9.6 | 9.6 | 7.8 | 9.3 |
乙 | 5.8 | 9.7 | 9.8 | 5.8 | 9.9 |
丙 | 4 | 6.2 | 8.5 | 9.9 | 9.9 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 中位数(万元) | 众数(万元) |
甲 | 9.3 | 9.6 | |
乙 | 8.2 | 5.8 | |
丙 | 7.7 | 8.5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.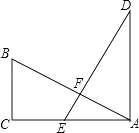
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系XOY中,A(-1,5),B(-1,0),C(-4,3).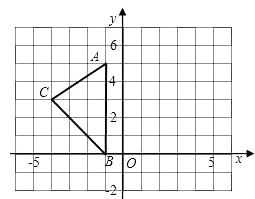
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com