
)如图所示,在⊙O中, ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
(1)求证:AC2=AB•AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.

(1)证明见解析;(2)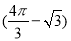 cm2.
cm2.
【解析】
试题分析:(1)由  ,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;
,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;
(2)连接OA,OC,利用同弧所对的圆心角等于圆周角的2倍,由∠B为60°,求出∠AOC为120°,过O作OE垂直于AC,垂足为点E,由OA=OC,利用三线合一得到OE为角平分线,可得出∠AOE为60°,在Rt△AOE中,由OA及cos60°的值,利用锐角三角函数定义求出OE的长,在Rt△AOE中,利用勾股定理求出AE的长,进而求出AC的长,由扇形AOC的面积-△AOC的面积表示出阴影部分的面积,利用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
(1)证明:∵ ,
,
∴∠ACD=∠ABC,又∠BAC=∠CAF,
∴△ACF∽△ABC,
∴ ,即AC2=AB•AF;
,即AC2=AB•AF;
(2)【解析】
连接OA,OC,过O作OE⊥AC,垂足为点E,

∵∠ABC=60°,
∴∠AOC=120°,
又OA=OC,
∴∠AOE=∠COE= ×120°=60°,
×120°=60°,
在Rt△AOE中,OA=2cm,
∴OE=OAcos60°=1cm,
∴AE=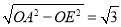 cm,
cm,
∴AC=2AE=2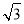 cm,
cm,
则S阴影=S扇形OAC﹣S△AOC=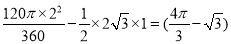 cm2.
cm2.
考点:1.扇形面积的计算;2.圆心角、弧、弦的关系;3.圆周角定理;4.相似三角形的判定与性质.


科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:解答题
某学校后勤人员到一家文具店给九年级的同学购买考试用文具包.文具店规定一次购买400个以上,可享受8折优惠,若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:选择题
在直角坐标系中,已知点A(-2,0)、B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以D、O、C为顶点的三角形与△AOB相似,这样的直线最多可以作( )
A.2条 B.3条 C.4条 D.6条
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与 轴相切于点C,与
轴相切于点C,与 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线 经过A,B,C三点.
经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:填空题
小明在某风景区的观景台O处观测到东北方向的P处有一艘货船, 该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东30 ,且与O相距6km的Q处.如图所示. 货船的航行速度是____________km/h.(结果用根号表示.)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:选择题
已知关于x的方程kx2+(1-k)x-1=0,下列说法正确的是( ).
A.当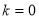 时,方程无解
时,方程无解
B.当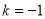 时,方程有两个相等的实数解
时,方程有两个相等的实数解
C.当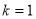 时,方程有一个实数解
时,方程有一个实数解
D.当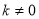 时,方程总有两个不相等的实数解
时,方程总有两个不相等的实数解
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:解答题
如图,已知矩形OABC中,OA=2,AB=4,双曲线 (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com