
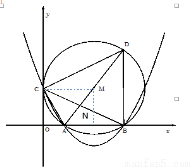
如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与 轴相切于点C,与
轴相切于点C,与 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线 经过A,B,C三点.
经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

(1)证明见解析;(2)8;(3)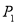
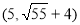 ,
,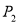
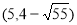 ,
,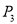
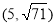 ,
,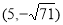 .
.
【解析】
试题分析:(1)利用切线的性质性质得出∠MCO=90°,进而得出∠OCA=∠MCD=∠MDC,再利用∠OCA+∠OAC=90°求出即可;
(2)利用圆周角定里以及平行线的性质,首先得出四边形COMN为矩形,进而求出BD=2MN;
(3)分别利用当CP=CB时,△PCB为等腰三角形,当BP=BC时,△PCB为等腰三角形,利用勾股定理求出即可.
(1)证明:如图1,连接MC,
∵⊙M与y轴相切于点C,∴CM⊥OC,
∴∠MCO=90°,
又∵∠ACD=90°
∴AD为⊙M的直径,
∵DM=CM,∠ACD+∠ADC=90°
∴∠MCD=∠MDC,
∵∠OCA+∠ACM=∠OCM=90°
∴∠MCD+∠ACM=90°
∴∠OCA=∠MCD=∠MDC
∵∠OCA+∠OAC=90°
∴∠OAC=∠CAD;
(2)【解析】
如图1,过点M作MN⊥OB于点N,
由(1)可知,AD是⊙M的直径,
∴∠ABD=90°,
∵MN⊥AB,∴∠MNA=90°,
∴MN∥BD,
∴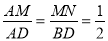 ,
,
∵∠OCM=∠CON=∠MNO=90°,
∴四边形COMN为矩形,
∴MN=CO=4,
∴BD=2MN=8;
(3)【解析】
抛物线的对称轴上存在点P,使ΔPBC是以BC为腰的等腰三角形.
在⊙M中,弧AC=弧AC ,∴∠ADC=∠ABC,
,∴∠ADC=∠ABC,
由(1)知,∠ADC=∠OCA,
∴∠OCA=∠OBC
在Rt△CAO和Rt△BOC中,
tan∠OCA=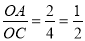
∴tan∠OBC=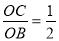
∴OB=2OC=8
∴A(2,0),B(8,0)
∵抛物线经过A,B两点,
∴A,B关于抛物线的对称轴对称,其对称轴为直线: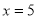 ;
;
当CP=CB=5时,△PCB为等腰三角形,
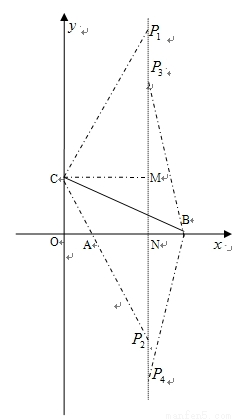
在Rt△COB中,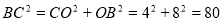
如图,在Rt△CM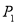 中,
中,
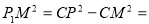 80-25=55
80-25=55
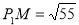 ,
,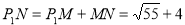
∴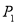
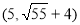
同理可求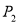 的坐标是
的坐标是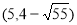
当BP=BC=5时,△PCB为等腰三角形,
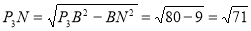
∴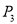
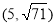
同理可得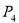 坐标为
坐标为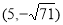
∴符合条件的点P有四个,坐标分别为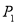
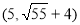 ,
,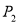
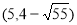 ,
,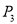
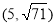 ,
,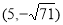 .
.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:解答题
甲、乙两船分别在相距120米的两平行航线上向东匀速行驶,小明站在甲船的船尾对着乙船拍照,此时他发现乙船的船尾在他们的西偏北30°方向,船头在他的西偏北45°方向.小明迅速用30秒时间走向船头,此时发现乙船船头在他的西偏北60°方向.已知甲船长20米,甲船的速度为600米/分.求乙船的长度和乙船的速度.(结果取整数)(参考数据: )
)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市九年级下学期入学考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
,则a的值是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:填空题
布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是____________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:选择题
点A在双曲线 上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
上,AB⊥x轴于B,且△AOB的面积为3,则k=( )
A.3 B.6 C.±3 D.±6
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:解答题
)如图所示,在⊙O中, ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
(1)求证:AC2=AB•AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
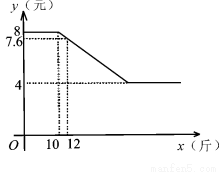
“兄弟餐厅”采购员某日到集贸市场采购草鱼,若当天草鱼的采购单价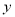 (元)与采购量
(元)与采购量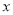 (斤)之间的关系如图,且采购单价不低于4元/斤.
(斤)之间的关系如图,且采购单价不低于4元/斤.
(1)直接写出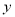 关于
关于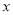 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)若这天他采购草鱼的量不多于20斤,那么这天他采购草鱼最多用去多少钱?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )

A.3米 B.4米 C.4.5米 D.6米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com