
分析 由抛物线表达式和三角形性质求出A、B、C各点坐标,就可以求出h或h的范围.
解答  解:由题A,B,C均在抛物线y=2x2上,并且斜边AB平行于x轴,
解:由题A,B,C均在抛物线y=2x2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
可设A(-$\sqrt{b}$,2b),B($\sqrt{b}$,2b),C(a,2a2),D(0,2b)
则因斜边上的高为h,
故:h=2b-2a2=2(b-a2),
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=$\sqrt{b}$,
∴a2+(2b-2a2)2=b,
方程两边平方得:4(b-a2)2=b-a2
即$\frac{1}{2}$h=h2
因h>0,得h=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 此题考查了二次函数的性质以及观察图形的能力,找到各点坐标之间的关系,巧妙地代换未知量是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
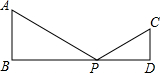 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{2}{3}$ | C. | 2 | D. | 任意有理数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com