
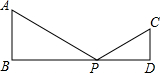
 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似? 分析 由题意得出∠B=∠D=90°,根据相似三角形的判定得出当$\frac{AB}{DP}=\frac{BP}{CD}$或$\frac{AB}{CD}=\frac{BP}{DP}$时,△PAB与△PCD是相似三角形,代入求出即可.
解答 解:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当$\frac{AB}{DP}=\frac{BP}{CD}$或$\frac{AB}{CD}=\frac{BP}{DP}$时,△PAB与△PCD是相似三角形,
∵AB=6,CD=4,BD=14,
∴$\frac{6}{14-BP}=\frac{BP}{4}$或$\frac{6}{4}=\frac{BP}{14-BP}$,
解得:BP=2或12或$\frac{42}{5}$,
即PB=2或12或$\frac{42}{5}$时,△PAB与△PCD是相似三角形.
点评 本题考查了相似三角形的判定的应用,注意有两种情况,用的知识点是:当两边对应成比例,且夹角相等的两三角形相似.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{x}$-x=1 | B. | (a2+1)x+b=0 | C. | ax2=b | D. | $\sqrt{2x+1}=5$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com