
分析 (1)根据一元一次方程的定义即可解决.
(2)根据一元二次方程的定义即可解决.
解答 解:(1)整理方程得到:(m2-1)x2-(m+1)x-3m=0,
∵方程是一元一次方程,
∴$\left\{\begin{array}{l}{{m}^{2}-1=0}\\{m+1≠0}\end{array}\right.$解得m=1,此时方程为-2x-3=0,x=-$\frac{3}{2}$,
∴m=1,方程的根为x=-$\frac{3}{2}$.
(2)由(1)可知::(m2-1)x2-(m+1)x-3m=0
∵方程是一元二次方程
点评 本题考查一元一次方程的定义,记住化简后只含有一个未知数,未知数的最高次数是1的方程就是一元一次方程,通常形式是ax+b=0,(a、b是常数,a≠0),属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-7m | B. | 2.5×106m | C. | 2.5×10-6m | D. | 2.5×10-8m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
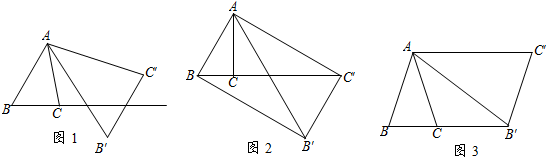
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
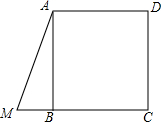 如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.
如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
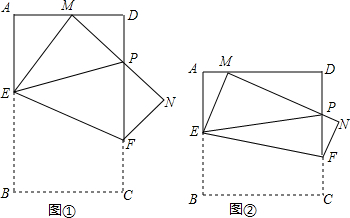
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
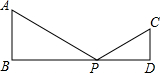 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com