
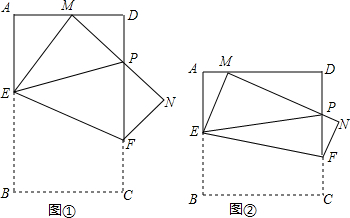
���� ��1���ٸ����۵������ʵõ�EM=EB�����������AEM���ܳ���
��ȡEP���е�Q������MQ���������ε���λ�����AE+DP=2MQ������ֱ�����������ʵó�EP=2MQ�����ɵó��𰸣�
��2������M��AD�����˶�ʱ����PDM���ܳ�û�з����仯��������AE=x��AM=y����BE=EM=k-x��MD=k-y����Rt��AEM�У��ɹ��ɶ����ã�AE2+AM2=EM2���ɵ�k2-y2=8x����֤��Rt��AEM��Rt��DMP��Ȼ�������������ε����ʣ���ô𰸣�
��� �⣺��1���١�MΪAD���ϵ��е㣬AD=2��
��AM=1��
�߾���ABCD��EF�۵���ʹ��B��AD���ϵĵ�M�غϣ���M����A��D�غϣ���
��EM=EB��
���AEM���ܳ�Ϊ��AE+EM+AM=AE+EB+1M=AB+AM=4+1=5��
�ʴ�Ϊ��5��
����ͼ�٣�ȡEP���е�Q������MQ��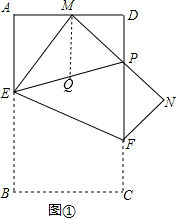
��MΪAD���е㣬
��AE+DP=2MQ��
���۵��ã���EMP=��B=90�㣬
��EP=2MQ��
��EP=AE+DP��
��2����AE=x��AM=y����BE=EM=k-x��MD=k-y��
��Rt��AEM�У��ɹ��ɶ����ã�AE2+AM2=EM2��
��x2+y2=��k-x��2��
��ã�k2-y2=2kx��
�ߡ�EMP=90�㣬
���AEM+��AME=90�㣬��DMP+��AME=90�㣬
���AEM=��DMP��
�ߡ�A=��D��
��Rt��AEM��Rt��DMP��
��$\frac{AE+AM+EM}{DM+DP+PM}=\frac{AE}{MD}$��
��$\frac{x+y+k-x}{DM+DP+PM}$=$\frac{x}{k-y}$��
��DM+DP+PM��x=��k+y����k-y��
��DM+DP+PM��x=k2-y2
��DM+DP+PM��x=2kx
DM+DP+PM=2k��
���PDM���ܳ��ǣ�2k��
���� ���⿼�����۵������ʡ������ε����ʡ����������ε��ж��������Լ����ɶ����������Ѷ����У�ע�������۵�ǰ��ͼ�εĶ�Ӧ��ϵ��ע���������ν��˼���뷽��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2=��m-1��2��b2=4m2��c2=��m+1��2 | B�� | a2=��m-1��2��b2=4m��c2=��m+1��2 | ||
| C�� | a2=��m-1��2��b2=2m��c2=��m+1��2 | D�� | a2=��m-1��2��b2=2m2��c2=��m+1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��a-1��=a2-1 | B�� | ��x-2����x+4��=x2-8 | C�� | ��x+2��2=x2+4 | D�� | ��x-2����x+2��=x2-4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com