
【题目】如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,
点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点
B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于
△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.

【答案】(1)2s或4s;(2)不存在.理由参见解析.
【解析】
试题分析:(1)设xs后,可使△PCQ的面积为8cm2,则PC=(6-x)cm,CQ=2xcm.根据三角形面积公式建立一元二次方程求解;(2)列△PCQ的面积等于△ABC面积的一半.建立一元二次方程,根据根的判别式,确定此方程是否有解,从而判断是否存在使△PCQ的面积等于ABC面积一半的时刻.
试题解析:(1)设xs后,可使△PCQ的面积为8cm2,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.则根据题意,得![]() ·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,得x1=2,x2=4. 所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2;(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.则根据题意,得
·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,得x1=2,x2=4. 所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2;(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.则根据题意,得![]() (6-x)·2x=
(6-x)·2x=![]() ×
×![]() ×6×8.整理,得x2-6x+12=0. 由于根的判别式小于0, 所以此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.
×6×8.整理,得x2-6x+12=0. 由于根的判别式小于0, 所以此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.


科目:初中数学 来源: 题型:
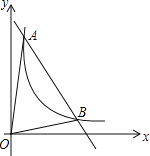
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
x | … | … | |||||
y | … | … |
(3)、若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,否则每超过1天罚款1 000元,甲、乙两人经商量后签订了该合同.
(1)正常情况下,甲、乙两人能否履行该合同?为什么?
(2)现两人合作了这项工程的75%,因别处有急事,必须调走1人,问调走谁更合适些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).

(1)当圆心O在∠BAD内部,∠ABO+∠ADO=60°时,∠BOD= ;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠A的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直径为![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,![]() ).
).
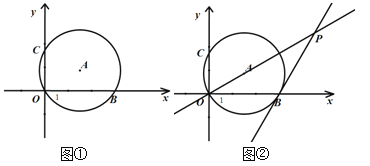
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com