
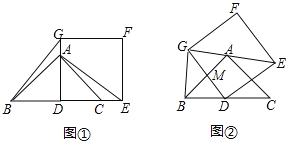
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥CE;
②设DG与AB交于点M,若AG:AE=3:4,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
试题分析:(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②设AG=3x,则AE=4x,即GE=7x,利用等腰直角三角形的性质得DG=![]() GE=
GE=![]() x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=![]() AB=
AB=![]() x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=
x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=![]() x,所以GM=
x,所以GM=![]() x,于是可计算出
x,于是可计算出![]() 的值.
的值.
试题解析:(1)证明:如图①,∵AD为等腰直角△ABC的高,∴AD=BD,∵四边形DEFG为正方形,∴∠GDE=90°,DG=DE,在△BDG和△ADE中,∵BD=AD,∠BDG=∠ADE,DG=DE,∴△BDG≌△ADE,∴BG=AE;
(2)①证明:如图②,∵四边形DEFG为正方形,∴△DEG为等腰直角三角形,∴∠1=∠2=45°,由(1)得△BDG≌△ADE,∴∠3=∠2=45°,∴∠1+∠3=45°+45°=90°,即∠BGE=90°,∴BG⊥GE;
②设AG=3x,则AE=4x,即GE=7x,∴DG=![]() GE=
GE=![]() x,∵△BDG≌△ADE,∴BG=AE=4x,在Rt△BGA中,AB=
x,∵△BDG≌△ADE,∴BG=AE=4x,在Rt△BGA中,AB=![]() =
=![]() =5x,∵△ABD为等腰直角三角形,∴∠4=45°,BD=
=5x,∵△ABD为等腰直角三角形,∴∠4=45°,BD=![]() AB=
AB=![]() x,∴∠3=∠4,而∠BDM=∠GDB,∴△DBM∽△DGB,∴BD:DG=DM:BD,即
x,∴∠3=∠4,而∠BDM=∠GDB,∴△DBM∽△DGB,∴BD:DG=DM:BD,即![]() x:
x:![]() x=DM:
x=DM:![]() x,解得DM=
x,解得DM=![]() x,∴GM=DG﹣DM=
x,∴GM=DG﹣DM=![]() x﹣
x﹣![]() x=
x=![]() x,∴
x,∴![]() =
=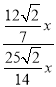 =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线 AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=10,BD=6,则四边形EFGH的面积为( )

A. 60 B. 30 C. 15 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
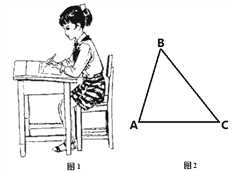
【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com