
 如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )| A. | $\frac{5}{16}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | $\frac{5}{4}$ |
分析 由E为线段AB中点,AD=DF找出ED=$\frac{1}{2}$BF,再由同弦的圆周角相等和对顶角相等得出△AED∽△CEB,由相似三角形的性质即可得出结论.
解答 解:∵点E为线段AB中点,AD=DF,
∴DE为△ABF的中位线,
∴ED=$\frac{1}{2}$BF.
∵∠DAE=∠BCE(同弦的圆周角相等),∠AED=∠CEB,
∴△AED∽△CEB,
∴$\frac{CB}{AD}$=$\frac{BE}{DE}$,
又∵$\frac{BE}{FB}$=$\frac{5}{8}$,ED=$\frac{1}{2}$BF,
∴$\frac{CB}{AD}$=$\frac{5}{4}$.
故选D.
点评 本题考查了三角形中位线定理、圆周角定理和相似三角形的判定与性质,解题的关键是:先找出ED=$\frac{1}{2}$BF,再由相似三角形的性质得出$\frac{CB}{AD}$=$\frac{BE}{DE}$.本题属于中档题,难度不大,但涉及到的知识点有点多,需要学生能熟练运用给知识点.


科目:初中数学 来源: 题型:选择题
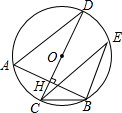 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
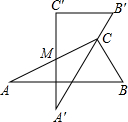 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
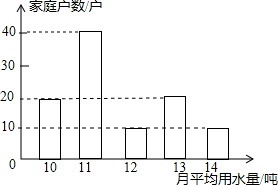 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com