
分析 (1)根据配方法解方程的方法可以解答此方程;
(2)根据直接开平方法可以解答此方程;
(3)根据因式分解法中的提公因式法可以解答此方程;
(4)根据因式分解法中的十字相乘法可以解答此方程.
解答 解:(1)x2-6x-4=0
移项,得
x2-6x=4
配方,得
(x-3)2=13
∴$x-3=±\sqrt{13}$,
∴$x=3±\sqrt{13}$
∴${x}_{1}=3-\sqrt{13},{x}_{2}=3+\sqrt{13}$;
(2)(x-3)2-9=0
移项,得
(x-3)2=9
∴x-3=±3
∴x=3±3
∴x1=0,x2=6;
(3)3x(x-2)=2(2-x)
移项,得
3x(x-2)+2(x-2)=0
∴(3x+2)(x-2)=0
∴3x+2=0或x-2=0,
解得,${x}_{1}=-\frac{2}{3},{x}_{2}=2$;
(4)3x2+5x-2=0
(3x-1)(x+2)=0
∴3x-1=0或x+2=0
解得,${x}_{1}=\frac{1}{3},{x}_{2}=-2$.
点评 本题考查解一元二次方程,解题的关键是明确解答一元二次方程的方法,巧妙的利用解方程的方法解答.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:填空题
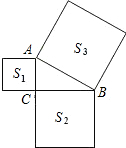 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
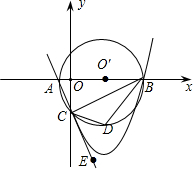 如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,
如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )| A. | $\frac{5}{16}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不赚不赔 | B. | 赔了12元 | C. | 赔了18元 | D. | 赚了18元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
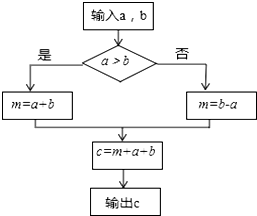 已知a、b为两个不相等的有理数,根据流程图中的程序:
已知a、b为两个不相等的有理数,根据流程图中的程序:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com