
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )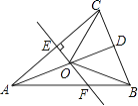
A.1对
B.2对
C.3对
D.4对
【答案】D
【解析】解:∵AB=AC,D为BC中点,
∴CD=BD,∠BDO=∠CDO=90°,
在△ABD和△ACD中,
 ,
,
∴△ABD≌△ACD;
∵EF垂直平分AC,
∴OA=OC,AE=CE,
在△AOE和△COE中,
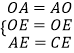 ,
,
∴△AOE≌△COE;
在△BOD和△COD中,
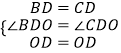 ,
,
∴△BOD≌△COD;
在△AOC和△AOB中,
 ,
,
∴△AOC≌△AOB;
故答案为:D.
根据等腰三角形的三线合一得出CD=BD,∠BDO=∠CDO=90°,从而利用SSS判断出△ABD≌△ACD;根据中垂线的性质得出OA=OC,AE=CE,从而利用SSS判断出△AOE≌△COE;再利用SAS判断出△BOD≌△COD;利用SSS判断出△AOC≌△AOB;


科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.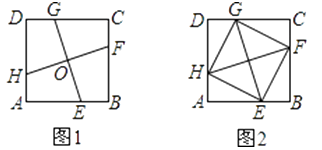
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
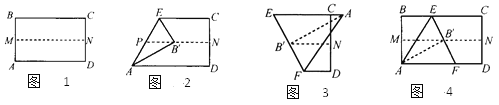
【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图:

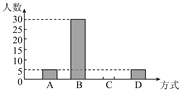
请根据图表所提供的信息回答下列问题:
(1)统计表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)若该校有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
(1)写出点M的实际意义;
(2)求第1小时内,y与t的一次函数表达式;
(3)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
(1)求抛物线的解析式;
(2)若PA:PB=3:1,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个球,其中7个黄球,8个黑球,5个红球,这些球只有颜色不同,其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列现象:①电梯的升降运动;②飞机在地面上沿直线滑行;③风车的转动;④钟摆的摆动.其中属于平移的是( )
A. ①③B. ①②C. ②③D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com