
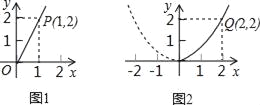
����Ŀ��ij��רҵ���ƻ�Ͷ����ֲ���ܼ���ľ�������г�������Ԥ�⣬��ֲ��ľ������y��Ͷ����x����������ϵ����ͼ1��ʾ����ֲ���ܵ�����y��Ͷ����x�ɶ��κ�����ϵ����ͼ2��ʾ��ע��������Ͷ�����ĵ�λ����Ԫ��
��1���ֱ��������y1��y2����Ͷ����x�ĺ�����ϵʽ��
��2�������λרҵ����8��Ԫ�ʽ�Ͷ����ֲ���ܺ���ľ�������ٻ�ö����������ܻ�ȡ����������Ƕ��٣�
��3���ڣ�2���Ļ�����Ҫ��֤������22��Ԫ���ϣ�����רҵ��Ӧ����Ͷ�ʣ�
���𰸡�(1)y1=2x,y2=![]() x2��x��0����(2) x=8ʱ��w�����ֵ��32 ;(3)������.
x2��x��0����(2) x=8ʱ��w�����ֵ��32 ;(3)������.
��������
��1���ɸ���ͼ�����ô���ϵ������⺯������ʽ��
��2������������=��ľ����+���������г�������ϵʽ������������ֵ��
��3����w=22���x��ֵ���ɵã�
��1����y1=kx����ͼ1��ʾ������y1=kx��ͼ�����1��2����
����2=k1��k=2��
������y1����Ͷ����x�ĺ�����ϵʽ��y1=2x��x��0����
�߸������ߵĶ�����ԭ�㣬
����y2=ax2��
��ͼ2��ʾ������y2=ax2��ͼ�����2��2����
��2=a22��
��ã�a=![]() ��
��
������y2����Ͷ����x�ĺ�����ϵʽ�ǣ�y=![]() x2��x��0����
x2��x��0����
��2����Ϊ��ֲ����x��Ԫ��0��x��8������Ͷ����ֲ��ľ��8��x����Ԫ��
w=2��8��x��+0.5 x2=![]() x2��2x+16=
x2��2x+16=![]() ��x��2��2+14��
��x��2��2+14��
��a=0.5��0��0��x��8��
�൱x=2ʱ��w����Сֵ��14��
��a=0.5��0��
�൱x��2ʱ��w��x�������������
��0��x��8��
�൱ x=8ʱ��w�����ֵ��32��
��3���������⣬��w=22ʱ��![]() ��x��2��2+14=22��
��x��2��2+14=22��
��ã�x=��2���ᣩ��x=6��
��w=![]() ��x��2��2+14��2��x��8�ķ�Χ����x������w����
��x��2��2+14��2��x��8�ķ�Χ����x������w����
��w��22��ֻ��Ҫx��6��
�ʱ�֤������22��Ԫ���ϣ�����רҵ��ӦͶ�ʳ���6��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ�λ�ڷ���������y��![]() ��y��
��y��![]() �ڵ�һ����ͼ���ϵ�����A��B����ԭ��O��ͬһֱ���ϣ���
�ڵ�һ����ͼ���ϵ�����A��B����ԭ��O��ͬһֱ���ϣ���![]() .
.
(1)��������y��![]() �ı���ʽ��
�ı���ʽ��
(2)����A��x���ƽ���߽�y��![]() ��ͼ���ڵ�C������BC�����ABC�������
��ͼ���ڵ�C������BC�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
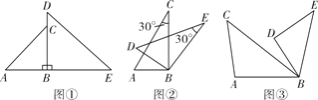
����Ŀ����ABC�͡�DBE���Ƶ�B��ת���������������Σ����С�ABC���DBE����A���DΪ��Ӧ�ǣ�
(1)��ͼ�٣�����ABC�͡�DBE�ֱ����ԡ�ABC���DBEΪ���ǵĵ���ֱ�������Σ�������������ת��ʹ��B��C��D��ͬһ��ֱ���ϵ�λ��ʱ����ֱ��д���߶�AD���߶�EC�Ĺ�ϵ��
(2)����ABC�͡�DBEΪ����30��ǵ�ֱ�������Σ���������������ת����ͼ�ڵ�λ��ʱ����ȷ���߶�AD���߶�EC�Ĺ�ϵ����˵�����ɣ�
(3)����ABC�͡�DBEΪ��ͼ�۵����������Σ��ҡ�ACB��������BDE���������Ƶ�B��ת�Ĺ����У�ֱ��AD��EC�нǵĶ����Ƿ�ı䣿�����ı䣬ֱ���ú���������ʽ�ӱ�ʾ�нǵĶ��������ı䣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
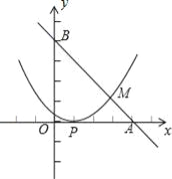
����Ŀ����֪����ͼ��ֱ��l����A��4��0����B��0��4�����㣬������y=a��x��h��2�Ķ���ΪP��1��0����ֱ��l�������ߵĽ���ΪM��
��1����ֱ��l�ĺ�������ʽ��
��2����S��AMP=3���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
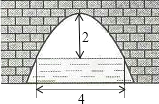
����Ŀ����ͼ��һ�������Ϊ��������״�Ĺ��ţ���ˮ���4mʱ�����������Ŷ�����ߵ㣩��ˮ��2m����ˮ���½�1mʱ��ˮ��Ŀ���Ϊ�� ��
A��3 B��2![]() C��3
C��3![]() D��2
D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ�ཻ�ڵ�D.AD��BC�ཻ�ڵ�F������BE��DC����֪EF=2��CD=5����AD=______________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D����ABC���Բ�ϵĵ㣬��B��Dλ��AC�����࣬DE��AB������ΪE��DE���ӳ��߽���Բ�ڵ�F��BG��AD������ΪG��BG��DE�ڵ�H��DC��FB���ӳ��߽��ڵ�P����PC=PB��
��1����֤����BAD=��PCB��
��2����֤��BG��CD��
��3������ABC���Բ��Բ��ΪO����AB=![]() DH����COD=23�������P�Ķ�����
DH����COD=23�������P�Ķ�����
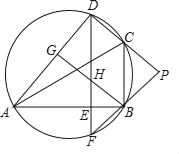
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=2x�ͷ�����������ͼ���ڵ�A��m����2����

��1�����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д������������ֵ���ڷ���������ֵʱ�Ա���x��ȡֵ��Χ��
��3����˫�����ϵ�C��2��n����OA����ƽ��![]() ����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABΪ��ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��ֱ��AB�ij�Ϊ4����BC=2����DAC=15�㣮
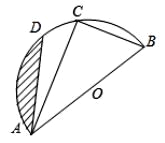
(1)����DAB�Ķ�����
(2)��ͼ����Ӱ���ֵ����(���������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com