
【题目】已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
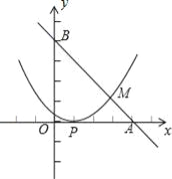
【答案】(1)y=﹣x+4;(2)y=2(x﹣1)2.
【解析】
(1)根据交点坐标先求直线l的函数解析式(2)抛物线的顶点坐标已知,设交点M的坐标,再根据S△AMP=3求出M的坐标,最后求出解析式.
(1)设一次函数解析式为y=kx+b,
把A(4,0),B(0,4)分别代入解析式得![]()
解得![]()
解析式为y=﹣x+4.
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴![]() (4﹣1)n=3,
(4﹣1)n=3,
解得,n=2,
把M(m,2)代入为2=﹣m+4得,m=2,
M(2,2),
∵抛物线y=a(x﹣h)2的顶点为P(1,0),
可得y=a(x﹣1)2,
把M(2,2)代入y=a(x﹣1)2得,2=a(2﹣1)2,解得a=2,函数解析式为y=2(x﹣1)2.


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
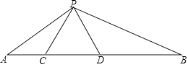
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 在边
在边![]() 上,
上,![]() ,
,![]() .
.
![]() 试说明
试说明![]() 与
与![]() 相似.
相似.
![]() 若
若![]() ,
,![]() ,
,![]() ,请你求出
,请你求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
![]() 小明猜想:若
小明猜想:若![]() ,
,![]() ,
,![]() ,只要
,只要![]() 与
与![]() 之间满足某种关系式,问题
之间满足某种关系式,问题![]() 中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出
中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出![]() 与
与![]() 所满足的关系式;若不同意,请说明理由.
所满足的关系式;若不同意,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
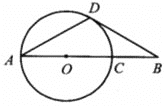
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D在⊙O上,连接AD,BD,∠A=∠B=30°.
证明:(1)BD是⊙O的切线
(2)如果BD=2求OC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).

(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
查看答案和解析>>
科目:初中数学 来源: 题型:
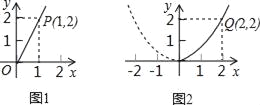
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y与投资量x成正比例关系,如图1所示:种植花卉的利润y与投资量x成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
(3)在(2)的基础上要保证获利在22万元以上,该园林专业户应怎样投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com