
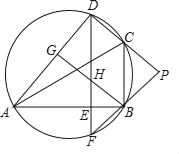
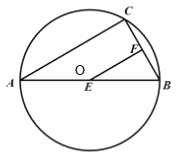
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)97°
【解析】
(1)根据邻补角定义和圆内接四边形对角互补、等边对等角即可证出结论.
(2)根据等边对等角得:∠PCB=∠PBC,由圆内接四边形的性质得:∠BAD+∠BCD=180°,从而得:∠BFD=∠PCB=∠PBC,根据平行线的判定得:BC∥DF,可得∠ABC=90°,AC是⊙O的直径,从而得:∠ADC=∠AGB=90°,根据同位角相等可得结论;
(3)先证明四边形BCDH是平行四边形,得BC=DH,根据特殊的三角函数值得:∠ACB=60°,最后由PC=PB,得出∠P=180°﹣2×(![]() )°=97°.
)°=97°.
(1)证明:如图1,
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∵∠ABC=90°,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,
∵AB=![]() DH,
DH,
∴tan∠ACB=![]() =
=![]() ,
,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=![]() (180°﹣23°)=(
(180°﹣23°)=(![]() )°,
)°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=(![]() )°,
)°,
∵PC=PB,
∴∠P=180°﹣2×(![]() )°=97°.
)°=97°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,BE=2DE=2![]() ,CD=
,CD=![]() .
.
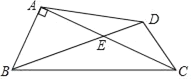
(1)求AB的长;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
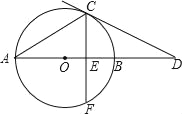
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
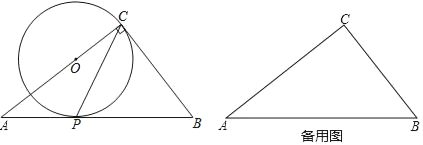
【题目】如图,在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P,AC=8,BC=6.
(1)当点O在AC上时,求证:2∠ACP=∠B;
(2)在(1)的条件下,求⊙O的半径.
(3)若圆心O在△ABC之外,则CP的变化范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体小服装店主准备在夏季来临前,购进甲、乙两种T恤.两种T恤的相关信息如表:
品牌 | 甲 | 乙 |
进价(元/件) | 45 | 80 |
售价(元/件) | 75 | 120 |
根据上述信息,该店决定用不少于6198元,但不超过6296元的资金购进这两种T恤共100件请解答下列问题:
(1)该店有哪几种进货方案?
(2)该店按哪种方案进货所获利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=4cm,点F是弦BC的中点,∠ABC=60°,若动点E以2cm/s的速度在线段AB上由A向B运动,连接EF,设运动时间为t(s),当△BEF是直角三角形时,t的值等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com