
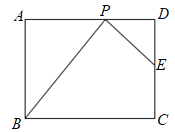
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,联结
上一点,联结![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() 点,将
点,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() ,若
,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为__________.
的长为__________.
【答案】![]() 或1
或1
【解析】
若![]() 为等腰三角形,则需分以下三种情况进行讨论,①若
为等腰三角形,则需分以下三种情况进行讨论,①若![]() ,根据BP=PD列出方程即可解出;②若
,根据BP=PD列出方程即可解出;②若![]() ,作出辅助线,证明△ABP≌△
,作出辅助线,证明△ABP≌△![]() (AAS),根据等腰三角形的性质得出PF=DF=
(AAS),根据等腰三角形的性质得出PF=DF=![]() ,再结合全等三角形的性质得到AP=PF,列出方程求解即可;③若
,再结合全等三角形的性质得到AP=PF,列出方程求解即可;③若![]() ,作出辅助线,在Rt△
,作出辅助线,在Rt△![]() 中运用勾股定理列出方程求解即可.
中运用勾股定理列出方程求解即可.
解:设AP=x,则PD=3-x,
∵PE⊥BP,
∴![]() 沿直线
沿直线![]() 翻折后,PE⊥
翻折后,PE⊥![]()
∵四边形ABCD是矩形,
∴∠A=90°,
∴![]() ,
,
①若![]()
即BP=PD
∴![]()
解得:![]()
②若![]() ,
,
过点![]() 作
作![]() F⊥AD交AD于点F,如下图1所示,
F⊥AD交AD于点F,如下图1所示,
则PF=DF=![]()
又∵![]() ,∠A=∠
,∠A=∠![]() FP,∠APB=∠
FP,∠APB=∠![]() PF,
PF,
∴△ABP≌△![]() (AAS)
(AAS)
∴AP=PF
即![]()
解得:![]()
③若![]()
过点![]() 作
作![]() F⊥AD交AD于点F,如图1所示,
F⊥AD交AD于点F,如图1所示,
∵![]() ,∠A=∠
,∠A=∠![]() FP,∠APB=∠
FP,∠APB=∠![]() PF,
PF,
∴△ABP≌△![]() (AAS)
(AAS)
∴PF=AP=x,![]()
∴FD=3-2x,![]()
在Rt△![]() 中,
中,![]() ,
,
即![]() ,此方程无解,故不存在
,此方程无解,故不存在![]() 这种情况,
这种情况,
综上所述:![]() 的长为
的长为![]() 或1
或1


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
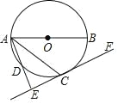
【题目】如图,AB为⊙O的直径,点C,D在⊙O上,且点C是![]() 的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
(1)求证:EF是⊙O的切线;
(2)连接BC,若AB=5,BC=3,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作AB两种型号的环保包装盒.已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个,且制作一个A型盒比制作一个B型盒要多用20%的材料.求制作每个A,B型盒各用多少材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市空气质量整治领导小组近期提出“保护好环境,拒绝冒黑烟”.某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能的公交车10辆.若购买
型两种环保节能的公交车10辆.若购买![]() 型公交车1辆,
型公交车1辆,![]() 型公交车2辆,共需400万元;若购买
型公交车2辆,共需400万元;若购买![]() 型公交车2辆,
型公交车2辆,![]() 型公交车1辆,共需350万元.
型公交车1辆,共需350万元.
(1)求购买![]() 型和
型和![]() 型公交车每辆各需多少万元?
型公交车每辆各需多少万元?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买
型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,![]() 的顶点均在格点上,建立平面直角坐标系后,点
的顶点均在格点上,建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
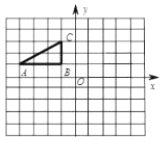
(1)先将![]() 向右平移5个单位,再向下平移1个单位后得到
向右平移5个单位,再向下平移1个单位后得到![]() ,试在图中画出图形
,试在图中画出图形![]() ;
;
(2)将![]() 绕点
绕点![]() 顺时针旋转90°后得到
顺时针旋转90°后得到![]() ,试在图中画出图形
,试在图中画出图形![]() ,并计算
,并计算![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
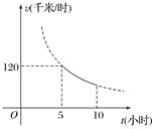
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
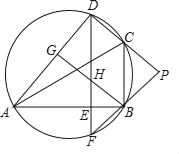
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com