
【题目】已知一次函数的图象经过点(2,1)和(0,﹣2).
(1)求出该函数图象与x轴的交点坐标;
(2)判断点(﹣4,6)是否在该函数图象上.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
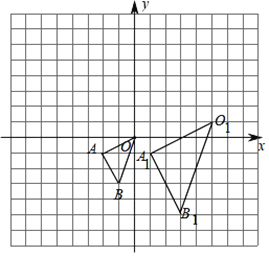
【题目】在如图所示的方格中,△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的位似比;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
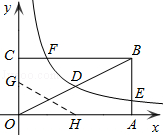
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.

(1)求![]() 的度数:
的度数:
(2)如图2,连接![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)abc>0;(3)b2-4ac>0;(4)5a+c=0;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有______(填序号).
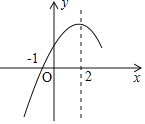
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,BE=2DE=2![]() ,CD=
,CD=![]() .
.
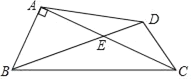
(1)求AB的长;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
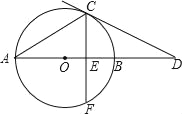
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com