
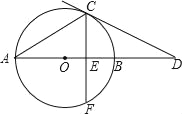
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】成都市空气质量整治领导小组近期提出“保护好环境,拒绝冒黑烟”.某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能的公交车10辆.若购买
型两种环保节能的公交车10辆.若购买![]() 型公交车1辆,
型公交车1辆,![]() 型公交车2辆,共需400万元;若购买
型公交车2辆,共需400万元;若购买![]() 型公交车2辆,
型公交车2辆,![]() 型公交车1辆,共需350万元.
型公交车1辆,共需350万元.
(1)求购买![]() 型和
型和![]() 型公交车每辆各需多少万元?
型公交车每辆各需多少万元?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买
型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
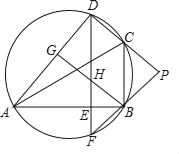
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级![]() 班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com