
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=ax2+bx£®a°Ÿ0£©π˝µ„E£®10£¨0£©£¨æÿ–ŒABCDµƒ±þAB‘⁄œþ∂ŒOE…œ£®µ„A‘⁄µ„Bµƒ◊Û±þ£©£¨µ„C£¨D‘⁄≈◊ŒÔœþ…œ£Æ…ËA£®t£¨0£©£¨µ±t=2 ±£¨AD=4£Æ
£®1£©«Û≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô Ω£Æ
£®2£©µ±tŒ™∫Œ÷µ ±£¨æÿ–ŒABCDµƒ÷Ð≥§”–◊Ó¥Û÷µ£ø◊Ó¥Û÷µ «∂ý…Ÿ£ø
£®3£©±£≥÷t=2 ±µƒæÿ–ŒABCD≤ª∂Ø£¨œÚ”“∆Ω“∆≈◊ŒÔœþ£Æµ±∆Ω“∆∫Ûµƒ≈◊ŒÔœþ”Îæÿ–Œµƒ±þ”–¡Ω∏ˆΩªµ„G£¨H£¨«“÷±œþGH∆Ω∑÷æÿ–Œµƒ√ʪ˝ ±£¨«Û≈◊ŒÔœþ∆Ω“∆µƒæý¿Î£Æ

°æ¥∞∏°ø£®1£©≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô ΩŒ™y=©Å![]() x2+
x2+![]() x£ª£®2£©µ±t=1 ±£¨æÿ–ŒABCDµƒ÷Ð≥§”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
x£ª£®2£©µ±t=1 ±£¨æÿ–ŒABCDµƒ÷Ð≥§”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ª£®3£©≈◊ŒÔœþœÚ”“∆Ω“∆µƒæý¿Î «4∏ˆµ•Œª£Æ
£ª£®3£©≈◊ŒÔœþœÚ”“∆Ω“∆µƒæý¿Î «4∏ˆµ•Œª£Æ
°æΩ‚Œˆ°ø£®1£©”…µ„Eµƒ◊¯±Í…Ë≈◊ŒÔœþµƒΩªµ„ Ω£¨‘Ÿ∞—µ„Dµƒ◊¯±Í£®2£¨4£©¥˙»Îº∆À„ø…µ√£ª
£®2£©”…≈◊ŒÔœþµƒ∂‘≥∆–‘µ√BE=OA=t£¨æð¥À÷™AB=10-2t£¨‘Ÿ”…x=t ±AD=-![]() t2+
t2+![]() t£¨∏˘æðæÿ–Œµƒ÷Ð≥§π´ Ω¡–≥ˆ∫Ø ˝Ω‚Œˆ Ω£¨≈‰∑Ω≥…∂•µ„ Ωº¥ø…µ√£ª
t£¨∏˘æðæÿ–Œµƒ÷Ð≥§π´ Ω¡–≥ˆ∫Ø ˝Ω‚Œˆ Ω£¨≈‰∑Ω≥…∂•µ„ Ωº¥ø…µ√£ª
£®3£©”…t=2µ√≥ˆµ„A°¢B°¢C°¢Dº∞∂‘Ω«œþΩªµ„Pµƒ◊¯±Í£¨”…÷±œþGH∆Ω∑÷æÿ–Œµƒ√ʪ˝÷™÷±œþGH±ÿπ˝µ„P£¨∏˘æðAB°ŒCD÷™œþ∂ŒOD∆Ω“∆∫Ûµ√µΩµƒœþ∂Œ «GH£¨”…œþ∂ŒODµƒ÷–µ„Q∆Ω“∆∫Ûµƒ∂‘”¶µ„ «P÷™PQ «°˜OBD÷–Œªœþ£¨æð¥Àø…µ√£Æ
£®1£©…Ë≈◊ŒÔœþΩ‚Œˆ ΩŒ™y=ax£®x-10£©£¨
°þµ±t=2 ±£¨AD=4£¨
°ýµ„Dµƒ◊¯±ÍŒ™£®2£¨4£©£¨
°ýΩ´µ„D◊¯±Í¥˙»ÎΩ‚Œˆ Ωµ√-16a=4£¨
Ω‚µ√£∫a=-![]() £¨
£¨
≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô ΩŒ™y=-![]() x2+
x2+![]() x£ª
x£ª
£®2£©”…≈◊ŒÔœþµƒ∂‘≥∆–‘µ√BE=OA=t£¨
°ýAB=10-2t£¨
µ±x=t ±£¨AD=-![]() t2+
t2+![]() t£¨
t£¨
°ýæÿ–ŒABCDµƒ÷Ð≥§=2£®AB+AD£©
=2[£®10-2t£©+£®-![]() t2+
t2+![]() t£©]
t£©]
=-![]() t2+t+20
t2+t+20
=-![]() £®t-1£©2+
£®t-1£©2+![]() £¨
£¨
°þ-![]() £º0£¨
£º0£¨
°ýµ±t=1 ±£¨æÿ–ŒABCDµƒ÷Ð≥§”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ª
£ª
£®3£©»ÁÕº£¨
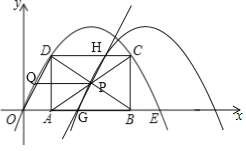
µ±t=2 ±£¨µ„A°¢B°¢C°¢Dµƒ◊¯±Í∑÷±Œ™£®2£¨0£©°¢£®8£¨0£©°¢£®8£¨4£©°¢£®2£¨4£©£¨
°ýæÿ–ŒABCD∂‘Ω«œþµƒΩªµ„Pµƒ◊¯±ÍŒ™£®5£¨2£©£¨
µ±∆Ω“∆∫Ûµƒ≈◊ŒÔœþπ˝µ„A ±£¨µ„Hµƒ◊¯±ÍŒ™£®4£¨4£©£¨¥À ±GH≤ªƒÐΩ´æÿ–Œ√ʪ˝∆Ω∑÷£ª
µ±∆Ω“∆∫Ûµƒ≈◊ŒÔœþπ˝µ„C ±£¨µ„Gµƒ◊¯±ÍŒ™£®6£¨0£©£¨¥À ±GH“≤≤ªƒÐΩ´æÿ–Œ√ʪ˝∆Ω∑÷£ª
°ýµ±G°¢H÷–”–“ªµ„¬‰‘⁄œþ∂ŒADªÚBC…œ ±£¨÷±œþGH≤ªø…ƒÐΩ´æÿ–Œµƒ√ʪ˝∆Ω∑÷£¨
µ±µ„G°¢H∑÷±¬‰‘⁄œþ∂ŒAB°¢DC…œ ±£¨÷±œþGHπ˝µ„P±ÿ∆Ω∑÷æÿ–ŒABCDµƒ√ʪ˝£¨
°þAB°ŒCD£¨
°ýœþ∂ŒOD∆Ω“∆∫Ûµ√µΩµƒœþ∂ŒGH£¨
°ýœþ∂ŒODµƒ÷–µ„Q∆Ω“∆∫Ûµƒ∂‘”¶µ„ «P£¨
‘⁄°˜OBD÷–£¨PQ «÷–Œªœþ£¨
°ýPQ=![]() OB=4£¨
OB=4£¨
À˘“‘≈◊ŒÔœþœÚ”“∆Ω“∆µƒæý¿Î «4∏ˆµ•Œª£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄±þ≥§Œ™5µƒ’˝∑Ω–ŒABCD÷–£¨“‘AŒ™“ª∏ˆ∂•µ„£¨¡ÌÕ‚¡Ω∏ˆ∂•µ„‘⁄’˝∑Ω–ŒABCDµƒ±þ…œ£¨«“∫¨±þ≥§Œ™3µƒÀ˘”–¥Û–°≤ªÕ¨µƒµ»—¸»˝Ω«–Œµƒ∏ˆ ˝Œ™£® £©

A.3B.4C.5D.6
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ„P «’˝∑Ω–ŒABCD±þAB…œ“ªµ„(≤ª”ÎA£¨B÷ÿ∫œ)£¨¡¨Ω”PD≤¢Ω´œþ∂ŒPD»∆µ„PÀ≥ ±’Ζ˝◊™90°„£¨µ√œþ∂ŒPE£¨¡¨Ω”BE£¨‘Ú°œCBEµ»”⁄( )

A. 75°„ B. 60°„ C. 45°„ D. 30°„
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø(10∑÷£©—ß–£◊È÷Ø—ß…˙≤Œº”◊€∫œ µº˘ªÓ∂Ø£¨À˚√«≤Œ”ΡÀƒ≥÷÷∆∑≈∆‘À∂Ø–¨µƒœ˙ €π§◊˜£¨“—÷™∏√‘À∂Ø–¨√øÀ´µƒΩ¯º€Œ™120‘™£¨Œ™—∞«Û∫œ µƒœ˙ €º€∏ÒΩ¯––¡À4Ãϵƒ ‘œ˙£¨ ‘œ˙«Èøˆ»Áœ¬±ÌÀ˘ æ£∫
µ⁄1ÃÏ | µ⁄2ÃÏ | µ⁄3ÃÏ | µ⁄4ÃÏ | |
€º€x£®‘™/À´£© | 150 | 200 | 250 | 300 |
œ˙ €¡øy£®À´£© | 40 | 30 | 24 | 20 |
£®1£©π€≤ϱÌ÷– ˝æð£¨x£¨y¬˙◊„ ≤√¥∫Ø ˝πÿœµ£ø«Î«Û≥ˆ’‚∏ˆ∫Ø ˝πÿœµ Ω£ª
£®2£©»Ù…Ã≥°º∆ªÆ√øÃϵƒœ˙ €¿˚»ÛŒ™3000‘™£¨‘Ú∆‰µ•º€∂®Œ™∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB£ΩAC£¨DŒ™»˝Ω«–Œƒ⁄“ªµ„£¨«“°˜DBCŒ™µ»±þ»˝Ω«–Œ£Æ
£®1£©«Û÷§£∫÷±œþAD¥π÷±∆Ω∑÷BC£ª
£®2£©“‘ABŒ™“ª±þ£¨‘⁄ABµƒ”“≤ýª≠µ»±þ°˜ABE£¨¡¨Ω”DE£¨ ‘≈–∂œ“‘DA£¨DB£¨DE»˝Ãıœþ∂Œ «∑ÒƒÐππ≥…÷±Ω«»˝Ω«–Œ£ø«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≥§∑Ω–ŒABCD÷–£¨°œDAB=°œB=°œC=°œD=90°„£¨AD=BC=6£¨ AB=CD=10£Æµ„EŒ™…‰œþDC…œµƒ“ª∏ˆ∂ص„£¨°˜ADE”ΰ˜AD°‰Eπÿ”⁄÷±œþAE∂‘≥∆£¨µ±°˜AD°‰BŒ™÷±Ω«»˝Ω«–Œ ±£¨DEµƒ≥§Œ™£®°°°°£©
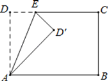
A.2ªÚ8B.![]() ªÚ18C.
ªÚ18C.![]() ªÚ2D.2ªÚ18
ªÚ2D.2ªÚ18
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“‘’˝∑Ω–ŒABCDµƒ±þAD◊˜µ»±þ°˜ADE£¨‘Ú°œBECµƒ∂» ˝ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨AD «°—Oµƒ÷±æ∂£¨ABŒ™°—Oµƒœ“£¨OP°ÕAD£¨OP”ÎABµƒ—”≥§œþΩª”⁄µ„P£¨π˝Bµ„µƒ«–œþΩªOP”⁄µ„C.
£®1£©«Û÷§£∫°œCBP=°œADB.
£®2£©»ÙOA=2£¨AB=1£¨«Ûœþ∂ŒBPµƒ≥§.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨¶§ABC÷–£¨AB=AC,Ω´A—ÿDE’€µ˛£¨ πA”ÎB÷ÿ∫œ£¨DEŒ™’€∫€£¨»Ù¶§BECŒ™µ»—¸»˝Ω«–Œ£¨‘Ú°œAµƒ∂» ˝ «_________.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com