
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75° B. 60° C. 45° D. 30°
【答案】C
【解析】
过E作AB的延长线AF的垂线,垂足为F,可得出∠F为直角,先利用AAS证明△ADP≌△PEF,根据全等三角形的对应边相等可得出AD=PF,AP=EF,再由正方形的边长相等得到AD=AB,由AP+PB=PB+BF,得到AP=BF,等量代换可得出EF=BF,即三角形BEF为等腰直角三角形,可得出∠EBF为45°,再由∠CBF为直角,即可求出∠CBE的度数.
过点E作EF⊥AF,交AB的延长线于点F,则∠F=90°,
∵四边形ABCD为正方形,
∴AD=AB,∠A=∠ABC=90°,
∴∠ADP+∠APD=90°,
由旋转可得:PD=PE,∠DPE=90°,
∴∠APD+∠EPF=90°,
∴∠ADP=∠EPF,
在△APD和△FEP中
∠ADP=∠FPE
∠A=∠F=90°
PD=EP,
∴△APD≌△FEP(AAS),
∴AP=EF,AD=PF,
又∵AD=AB,
∴PF=AB,即AP+PB=PB+BF,
∴AP=BF,
∴BF=EF,又∠F=91°,
∴△BEF为等腰直角三角形,
∴∠EBF=45°,又∠CBF=91°,
则∠CBE=45°.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数y=![]() 的图象的一个分支,对于给出的下列说法:
的图象的一个分支,对于给出的下列说法:

①常数k的取值范围k>2;②另一分支在第三象限;③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;④在函数图象的某一分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2.其中正确的是__________.(在横线上填上正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A.将y=
(x>0)的图象交于点A.将y=![]() x的图象向下移6个单位后与双曲线y=
x的图象向下移6个单位后与双曲线y=![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求点C的坐标;
(2)若![]() =2,求反比例函数的表达式.
=2,求反比例函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E, 若∠CAE=15°则∠BOE=( )

A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
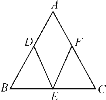
【题目】如图,△ABC中,AB=AC,点D,E,F分别是△ABC边AB,BC,AC的中点,连接DE,EF,要使四边形ADEF是正方形,还需增加条件:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F,G,求证:PF+PG=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知![]() 于点D,AE平分
于点D,AE平分![]()
(1)试探究![]() 与
与![]() 的关系;
的关系;
(2)若F是AE上一动点,当F移动到AE之间的位置时,![]() ,如图2所示,此时
,如图2所示,此时![]() 的关系如何?
的关系如何?
(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,![]() ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为 ![]() ,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成|x2-x1|或|y2-y1|.
,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成|x2-x1|或|y2-y1|.
(1)已知A(3,5),B(-2,-1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(-3,2),C(3,2),你能断定此三角形的形状吗?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com