练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

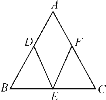
    【题目】如图，△ABC中，AB＝AC，点D，E，F分别是△ABC边AB，BC，AC的中点，连接DE，EF，要使四边形ADEF是正方形，还需增加条件：_______．

    【答案】∠A＝90°

    【解析】

    由已知点D、E、F分别是△ABC的边AB、BC、AC的中点，并且AB=AC，从而得到四边形ADEF是菱形，由一角为直角的菱形为正方形．故需要添加∠A=90°.

    ∵点D、E、F分别是△ABC的边AB、BC、AC的中点，

    ∴EF=AD=BD=AB, DE=AF=CFD=AC,

    ∵AB=AC,

    ∴AD=DE=EF=AF,

    ∴四边形ADEF是菱形.

    如果有一角为直角，菱形就成为正方形．故添加∠A=90°即可.

    故答案为：∠A=90°(此题答案不唯一)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知点D为等腰直角△ABC内一点，∠ACB＝90°，AD＝BD，∠BAD＝30°，E为AD延长线上的一点，且CE＝CA，若点M在DE上，且DC＝DM．则下列结论中：①∠ADB＝120°；②△ADC≌△BDC；③线段DC所在的直线垂直平分线AB；④ME＝BD；正确的有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店分两次购进两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：

    购进数量(件)

    购进所需费用(元)

    第一次

    30

    40

    3800

    第二次

    40

    30

    3200

    (1) 求两种商品每件的进价分别是多少元？

    (2) 商场决定种商品以每件30元出售，种商品以每件100元出售．为满足市场需求，需购进两种商品共1000件，且种商品的数量不少于种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，∠A=30°，取斜边AB的中点E，易得△BCE是等边三角形，从而得到“直角三角形中，30°角所对的直角边等于斜边的一半”利用这个结论解决问题：

    如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，若动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动．过点P作PD⊥AC于点D（点P不与点A.B重合），作∠DPQ=60°，边PQ交射线DC于点Q．设点P的运动时间为t秒．

    （1）用含t的代数式表示线段DC的长；

    （2）当线段PQ的垂直平分线经过△ABC一边中点时，直接写出t的值．

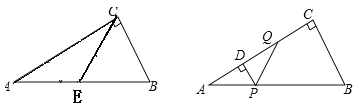
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P是正方形ABCD边AB上一点(不与A，B重合)，连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于( )

    A. 75° B. 60° C. 45° D. 30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEB中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是

    A．BC=EC，∠B=∠E B．BC=EC，AC=DC

    C．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA=CQ，连PQ交AC边于

    点D．

    （1）证明：PD=DQ．

    （2）如图2，过P作PE⊥AC于E，若AB=2，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE．下列说法①△BDF≌△CDE；②△ABD和△ACD面积相等；③BF∥CE；④CE=BF．其中正确的有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（9分）如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）

    查看答案和解析>>

    同步练习册答案