
【题目】如图1,P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于
点D.

(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=2,求DE的长.
【答案】答案见解析.
【解析】
(1)利用平行线的性质结合全等三角形的判定与性质得出即可;
(2)过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=![]() AC即可.
AC即可.
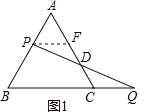
证明:如图1,过点P作PF∥BC交AC于点F;
∵PF∥BC,
∴△APF∽△ABC,
又∵△ABC是等边三角形,
∴△APF是等边三角形,
∴∠APF=∠BCA=60°,AP=PF=AF=CQ,
∴∠FDP=∠DCQ,∠FDP=∠CDQ,
∵在△PDF和△QDC中,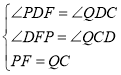
∴△PDF≌△QDC(AAS),
∴PD=DQ;
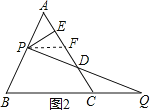
(2)解:如图2,过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
由(1)可知∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,∴AE+CD=DE=![]() AC,又∵AC=2,
AC,又∵AC=2,
∴DE=1.


科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在![]() 中,把AB绕点A顺时针旋转
中,把AB绕点A顺时针旋转![]() 得到
得到![]() ,把AC绕点A逆时针旋转
,把AC绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 当
当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 边
边![]() 上的中线AD叫做
上的中线AD叫做![]() 的“旋补中线”,点A叫做“旋补中心”.
的“旋补中线”,点A叫做“旋补中心”.
特例感知:
![]() 在图2,图3中,
在图2,图3中,![]() 是
是![]() 的“旋补三角形”,AD是
的“旋补三角形”,AD是![]() 的“旋补中线”.
的“旋补中线”.
![]() 如图2,当
如图2,当![]() 为等边三角形时,AD与BC的数量关系为
为等边三角形时,AD与BC的数量关系为![]() ______BC;
______BC;
![]() 如图3,当
如图3,当![]() ,
,![]() 时,则AD长为______.
时,则AD长为______.
猜想论证:
![]() 在图1中,当
在图1中,当![]() 为任意三角形时,猜想AD与BC的数量关系,并给予证明.
为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
![]() 如图4,在四边形ABCD,
如图4,在四边形ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在四边形内部是否存在点P,使
在四边形内部是否存在点P,使![]() 是
是![]() 的“旋补三角形”?若存在,给予证明,并求
的“旋补三角形”?若存在,给予证明,并求![]() 的“旋补中线”长;若不存在,说明理由.
的“旋补中线”长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A.将y=
(x>0)的图象交于点A.将y=![]() x的图象向下移6个单位后与双曲线y=
x的图象向下移6个单位后与双曲线y=![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求点C的坐标;
(2)若![]() =2,求反比例函数的表达式.
=2,求反比例函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D,E,F分别是△ABC边AB,BC,AC的中点,连接DE,EF,要使四边形ADEF是正方形,还需增加条件:_______.
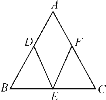
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F,G,求证:PF+PG=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知![]() 于点D,AE平分
于点D,AE平分![]()
(1)试探究![]() 与
与![]() 的关系;
的关系;
(2)若F是AE上一动点,当F移动到AE之间的位置时,![]() ,如图2所示,此时
,如图2所示,此时![]() 的关系如何?
的关系如何?
(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,![]() ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度数
(2)写出∠DAE与∠C-∠B的数量关系,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com